En el siglo XVII se produjo la revolución científica que cambió la forma de entender el universo. Los avances fueron espectaculares:
- Consolidación del sistema heliocéntrico
- Descubrimiento de las leyes de Kepler
- Determinación del tamaño del sistema solar
- La mecánica celeste de Newton
Me voy a centrar sobre todo en la contribución de la geometría a la astronomía para obtener un modelo de nuestro sistema solar y más allá.
SISTEMA HELIOCÉNTRICO
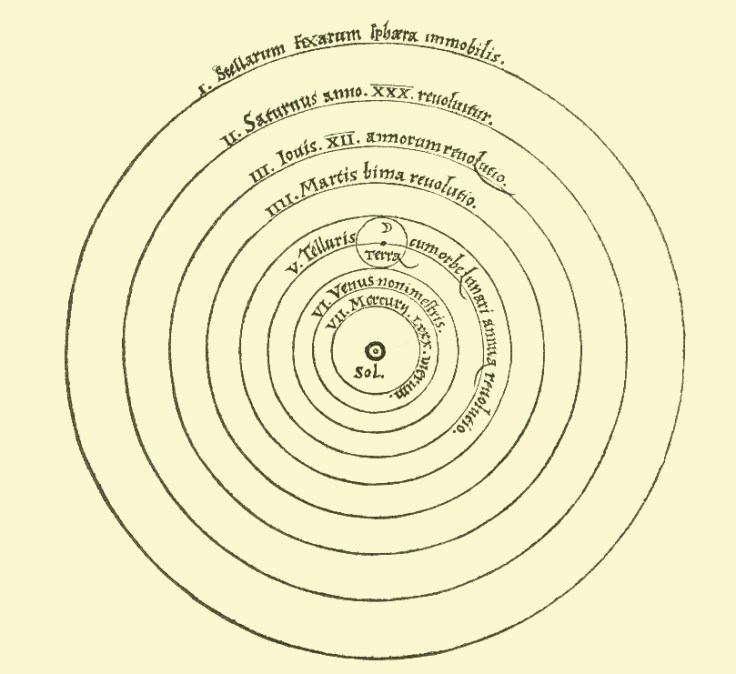
El sistema geocéntrico ideado por la cosmología griega dio paso después de dos milenios al sistema heliocéntrico. La Tierra dejaba de estar estática, giraba sobre su eje y además giraba alrededor del Sol que se posicionaba en el centro del universo. Este sistema fue desarrollado por Copérnico y defendido por Galileo.
Galileo en 1609 y 1610 aportó además las pruebas empíricas cuando con su telescopio de 3 cm de diámetro apuntó al cielo:
- La Luna no era una esfera perfecta, tenía cráteres y montañas
- El Sol tenía manchas y además giraba sobre sí mismo
- Venus tenía fases igual que la Luna
- y sobre todo Júpiter tenía nuevos mundos girando alrededor
Todo el universo aristotélico se tambaleo desde sus cimientos.
#
ÓRBITAS CÓNICAS
Las órbitas de los planetas en el sistema propuesto por Copérnico seguían siendo circulares.
APOLONIO (IIIa. C.)
En el Siglo de Oro (III a. C.) de la ciencia griega despuntó la geometría con el tratado «Los elementos» de Euclides. Este tratado recopilaba de forma lógica y estructurada todo el saber aritmético y geométrico acumulado por los griegos. En el mismo siglo confluyen también dos figuras sobresalientes: Arquímedes y Apolonio.
Aunque el nombre de Euclides ha perdurado durante siglos por su compendio geométrico, Apolonio fue al igual que Arquímedes un geómetra totalmente original. Destacaré algunos aspectos de su obra relacionados con el tema tratado.
- Tratado geométrico sobre las curvas cónicas. Las curvas cónicas obtenidas al seccionar un cono son: la elipse, la parábola y la hipérbola. Menecmo en el siglo anterior empezó a analizar secciones a diferentes conos, pero Apolonio hace un análisis pormenorizado en cuanto a su definición y propiedades.
Apolonio ni se planteo que estas curvas cónicas podrían ser aplicadas al movimiento de los astros y en concreto a los planetas. En su época la cosmología griega imperaba una trayectoria perfecta: la circunferencia.
- El dominio que tenía de la geometría le permitió ser el primero en utilizar epiciclos y deferentes para explicar la retrogradación de los planetas y su cambio de brillo.
Posteriormente este sistema se iría perfeccionando para dar cuenta, cada vez con más precisión, de los movimientos de los astros tanto en el sistema geocéntrico como en los inicio del heliocentrismo. Hiparco mejoró el sistema de Apolonio e incorporaría las excentricas, Ptolomeo añadiría a las excéntricas los ecuantes, que permitían dar cuenta de la diferente velocidad de los planetas por la eclíptica y ajustes más finos en correspondencia con los movimientos reales de los astros. Copérnico, y antes de él algunos astrónomos árabes, eliminaron los ecuantes, no obstante, Copérnico utilizaba todavía cuarenta circunferencias o más para predecir el movimiento de los astros. Hoy en día, que tenemos una concepción física del universo, nos parecen soluciones artificiales, pero en aquel momento esos artificios geométricos fueron capaces de predecir el movimiento de los planetas e incluso los eclipses. Todo esto desapareció cuando Kepler formuló sus tres leyes.
Para un análisis más profundo os recomiendo este libro: La rebelión de los astrónomos. Copérnico y Kepler, García Hourcade, J. L. (2000). Madrid: Nivola.
#
KEPLER
Kepler además de astrónomo era un gran geómetra. Aunque parezca mentira esto fue un hándicap al principio porque le mantuvo encorsetado durante mucho tiempo en ideas filosóficas como que la trayectoria circular es la curva perfecta o incluso jugar con los sólidos platónicos para obtener la separación de las esferas que movían los planetas; pero al final cedió a los datos empíricos que le mostraban otro camino menos «perfecto».

Utilizó los datos de las meticulosas observaciones del gran astrónomo Tycho Brahe (con precisiones de hasta 2′ de arco), sobre todo las de Marte que era el planeta que peor le encajaba en una órbita circular, para determinar sus tres leyes que rigen las órbitas de los planetas del sistema solar.
- Las tres leyes de Kepler:
1ª – Los planetas giran en órbitas elípticas alrededor del Sol (situado en uno de los focos de la elipse).
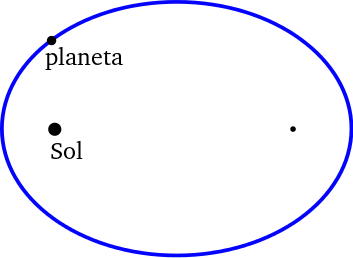
2ª – Se barren áreas iguales en tiempos iguales (los planetas van más rápido en su desplazamiento por su órbita cuando están cerca del Sol).

3ª – Relación entre las distancias relativas de las órbitas al Sol y el periodo que tardaban los planetas en completar dicha órbita.
P2/a3=cte., siendo P el periodo orbital y a el semieje mayor de la elipse (distancia media del planeta al Sol)
#
EL PARALAJE Y LA ESCALA DEL SISTEMA SOLAR
La Geometría sería una herramienta poderosísima en manos de los astrónomos.
LOS GRIEGOS
A pesar de sus instrumentos rudimentarios, fueron capaces de medir tamaños y distancias de la Tierra, La Luna y el Sol. Para ello utilizaron sobre todo triangulación y relaciones de proporción de figuras semejantes (misma forma pero distinto tamaño).
Aristarco consiguió obtener los tamaños y distancias de la Luna y el Sol en proporción al tamaño de la Tierra que aún estaba por determinar. Eratóstenes, fue capaz de medir el tamaño de la Tierra por primera vez, consiguiendo una precisión asombrosa. En el siglo siguiente Hiparco, utilizando el dato de Eratóstenes y aplicando el método de Aristarco con alguna variación, daría con bastante precisión la distancia a la Luna y con poca precisión la distancia al Sol. Ptolomeo mejoraría algo los cálculos de Hiparco respecto a la Luna, la cual midió directamente por paralaje, pero erróneamente dió por bueno el tamaño de la Tierra de Posidonio (siglo I) que era las tres cuartas partes del diámetro de Eratóstenes, dato que como ya comentamos sería aprovechado por Colón.
#
MEDICIÓN DE ERATÓSTENES
Eratóstenes sabía que en el solsticio de verano, en Siena (Asuán) el Sol se situaba al mediodía en el cénit (el Sol se reflejaba en el fondo de un pozo), el mismo día en Alejandría, situada más o menos en el mismo meridiano, un gnomon proyectaba una sombra. Esa diferencia de altura del Sol era otra evidencia más de que la Tierra era esférica, pero Eratóstenes iría más allá, ideó un método para medir su tamaño. Relaciono dos triángulos semejantes (ángulos iguales): el pequeño formado por el gnomon y su sombra y el grande formado por la unión de los lugares con el centro de la Tierra (ver imagen). Dibujando el triángulo pequeño pudo determinar su ángulo de 1/50 de circunferencia, por tanto, como el ángulo en el centro de la Tierra es el mismo ya sólo le faltaba tener la distancia entre los dos lugares y multiplicarla por 50. Esa distancia pudo obtenerla entrenando a una persona a dar pasos de igual longitud o probablemente ya estuviera registrada esa distancia en la biblioteca de Alejandría. Al final obtuvo un resultado de 250 000 estadios para el perímetro de la Tierra, aunque luego lo cambió por 252000 para que al dividir por 360 se obtuviera un número de estadios entero en correspondencia con un grado. Hay cierta controversia con el estadio utilizado (egipcio de 157’5 m, olímpico de 176’4 o el ático-italiano de 185 m),por tanto, la medición puede variar respecto al perímetro actual entre un 1% y un 15%. Hoy sabemos que el perímetro de la Tierra medido en un meridiano (circunferencia polar) es de 40008 Km, el valor obtenido por Eratóstenes fue una excelente aproximación en uno de los primeros intentos de dar tamaño a nuestro orbe.
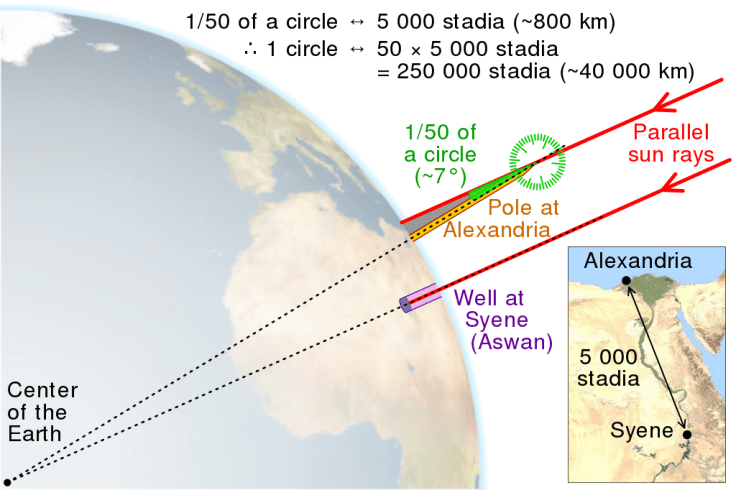
Imagen: cmglee, David Monniaux, jimht at shaw dot ca CC BY-SA
Si quieres saber como la ciencia islámica afrontó nuevos métodos de medición de la Tierra pincha aquí.
#
MÉTODO UTILIZADO POR ARISTARCO Y POSTERIORMENTE POR HIPARCO
El proceso seguido por Aristarco fue el siguiente:
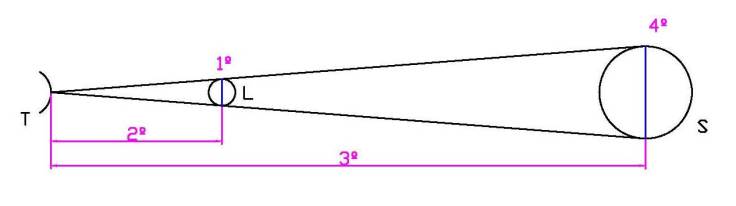
Imagen: JC Asensi CC BY-SA-NC
1º – Observando un eclipse lunar se compara el tamaño de la Luna con el de la sombra que proyecta la Tierra sobre ella.

Aristarco conocía el tiempo que tardaba la Luna en «recorrerse a si mima» sobre el fondo de estrellas (este tiempo era aproximadamente de una hora) y, por tanto, podía estimar el tiempo que tardaba la Luna en recorrer la sombra de la Tierra. De esta manera obtuvo el diámetro de la Luna en relación al diámetro de la Tierra. Posteriormente Hiparco calcaría directamente las circunferencias en un material transparente para compararlas.
2º – A partir del tamaño angular con el que observamos la Luna (aproximadamente medio grado) y el tamaño antes calculado Aristarco pudo calcular la distancia a nuestro satélite natural en relación al diámetro de la Tierra.
3º – La distancia al Sol la pudo calcular a partir de la distancia a la Luna (T-L) al medir el ángulo de separación entre la Luna y la Tierra (α) un día de cuarto creciente o decreciente. Aquí tuvo un error de casi 3º en la medición del ángulo, algunos lo atribuyen a la falta de precisión de los instrumentos de la época, pero esos instrumentos podrían tener precisiones de un grado, por lo que parece más probable que el error se deba a la determinación del terminador en la mitad justa del círculo.
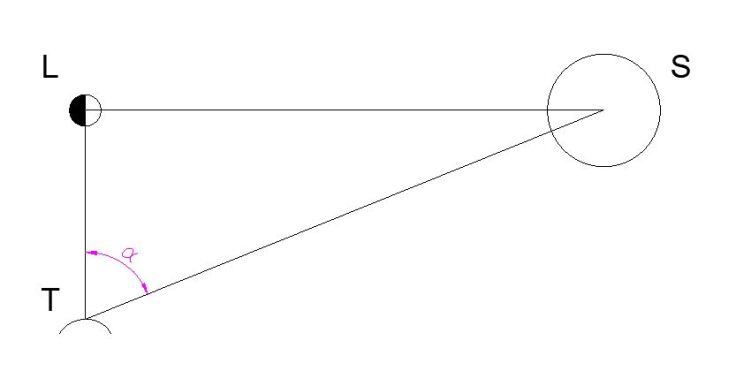
4º – Con los tres datos anteriores, por semejanza (ya que la Luna y el Sol tienen una amplitud angular similar en torno a los 30′ de arco), pudo establecer el tamaño del Sol.
Estimó una distancia a la Luna de 20 veces el diámetro de la Tierra (hoy sabemos que son 30). Los aparatos de medición de la época no permitieron medir correctamente la distancia al Sol; Aristarco obtuvo un diámetro del Sol 8 veces mayor que el de la Tierra (hoy sabemos que su diámetro es 100 veces mayor), pero pudo ser un dato fundamental para sostener que el Sol debía ser el centro del universo.
Con este método Hiparco consiguió estimar la distancia a la Luna entre 31 y 36 veces el diámetro de la Tierra.
PARALAJE LUNAR, HIPARCO Y PTOLOMEO
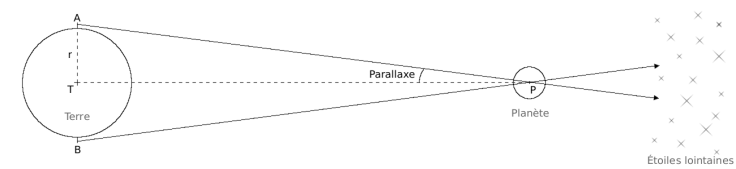
Hiparco sabía que un eclipse de Sol no se veía igual en dos lugares diferentes de la Tierra. La Luna pasaba delante del Sol y ofrecía un paralaje respecto al Sol a diferentes observadores. Se dispuso, por tanto, a emplear un segundo método para estimar la distancia a la Luna.
Los datos de un eclipse de su época ofrecían un eclipse total en Helesponto y otro parcial en Alejandría con la Luna cubriendo 4/5 del Sol. Los cálculos dependían mucho de esta apreciación y, por tanto, fueron algo más erróneos obteniendo entre 30 y 40 diámetros terrestres.
Ptolomeo calcula la distancia a la Luna por paralaje lunar obteniendo un valor de 30 diámetros terrestres.
El Sol y los planetas estaban tan lejos que no se podía apreciar ningún paralaje a simple vista.
EL PARALAJE DE MARTE Y VENUS
Después de que Kepler estableciera sus tres leyes se podía establecer la relación entre las distintas órbitas de los planetas del sistema solar y su distancia al Sol, pero faltaba una medición precisa para poder dar escala a todo el conjunto. La distancia al Sol era difícil de determinar por su lejanía, por tanto, los objetivos pasaron a ser los planetas más cercanos a la Tierra: Venus y Marte. El telescopio, recién descubierto, pasaría a ser esencial para determinar el paralaje de estos planetas. Otro elemento fundamental sería utilizar una base del triángulo mayor, separando los lugares de observación.
En 1671 G. Cassini obtiene el paralaje de Marte al mandar observarlo desde dos lugares simultáneamente, París y la Guayana francesa. Obtiene al final una distancia de la Tierra al Sol de 140 millones de Km.
En 1761 y 1769 se organizaron expediciones por todo el mundo para observar los tránsitos de Venus y así poder determinar la distancia a la que se encontraba. El método utilizado fue ideado por Halley en 1716 y se obtuvo un valor de 153 millones de km (hoy tomamos un valor de 149,6 millones de Km), con un error de únicamente un 2%. La distancia de la Tierra al Sol, la unidad astronómica (1UA) había quedado determinada.
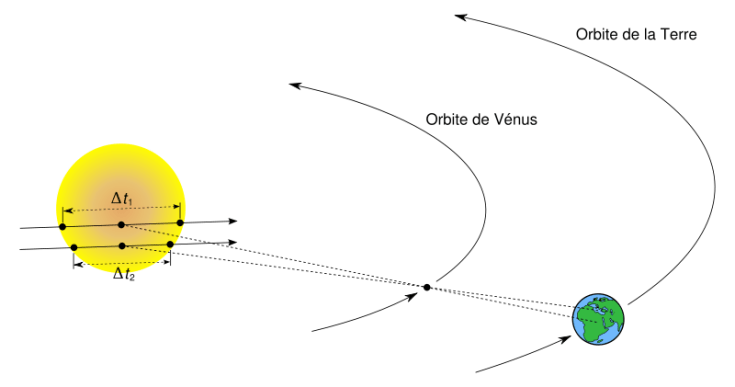
Estos cálculos se apoyaron en el nuevo perímetro obtenido de la Tierra de 40030 Km obtenido por Picard en 1668, medida obtenida por triangulación geodésica de 2º de meridiano.

La triangulación geodésica permitía medir distancias grandes concatenando triángulos.
Se partía de una única medida más pequeña tomada con mucha precisión (CE), después se medían los ángulos de los triángulos, al resolver matemáticamente estos triángulos esféricos se obtenían sus distancias y, por tanto, la distancia entre dos lugares situados en el meridiano (AB).
En 1666 la Academia de las Ciencias de París se puso el objetivo de medir la Tierra.
Picard, apoyado en el método ideado por G. Frisius el siglo anterior y ya aplicado por algún contemporáneo, estuvo dos años triangulando entre Amiens y Malvoisine al sur de París. El resultado fue excelente con un error menor a un uno por mil.
Se había dado por fin escala a todo el sistema solar, otro de los logros de la revolución científica que había sido culminado en el siglo de las luces.

Habría que esperar al siglo XIX para que Bessel midiera la primera paralaje estelar a una estrella cercana, obteniendo una distancia impensable de 10,4 años luz. Bessel tendría nuevamente que ampliar la base del triangulo que separa las observaciones, utilizando la paralaje anual que nos permite ampliar la base observando seis meses después la misma estrella.
Hoy podemos medir la distancia a un planeta con un radar que detecte la reflexión de una señal electromagnética en su su superficie, pero las distancias enormes a las estrellas cercanas se siguen midiendo por paralaje, para ello se utilizan satélites dotados de instrumentos de altísima precisión como Hipparcos y Gaia de la ESA. Estas medidas a las estrellas cercanas por geometría son la base de la determinación de los siguientes escalones en la obtención de distancias en el universo con métodos propios de la astrofísica (brillo de estrellas variables cefeidas, supernovas, desplazamiento al rojo, lentes gravitacionales,…).
LA MECÁNICA CELESTE Y EL MOVIMIENTO ORBITAL
NEWTON
Animado por Halley publica en 1687 Philosophiae naturalis principia mathematica. Descubre porqué los planetas siguen la trayectoria elíptica descrita por Kepler, desarrollando sus leyes del movimiento y la Ley de la gravitación universal. También explicará las mareas y la razón de la precesión de los equinoccios observada por Hiparco.
Su frase célebre: “Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes”.
Por las variaciones orbitales de Urano (descubierto por W. Herschel en 1781) y aplicando la mecánica celeste Adams y Le Verrier independientemente supieron donde apuntar su telescopio para observar un nuevo planeta: Neptuno.
HALLEY
En 1705 determinó la orbita del cometa Halley y predijo su reaparición.
#
LA EXCENTRICIDAD DE UNA CÓNICA
Una órbita cónica (de un planeta, satélite natural o artificial, cometa, sonda,…) viene definida por su excentricidad.
e=c/a
a es el semieje mayor en el caso de la elipse o el semieje real en el caso de la hipérbola
c es la separación del foco al centro de la cónica
La circunferencia tiene e=0, la elipse e<1, la parábola e=1 y la hipérbola e>1.
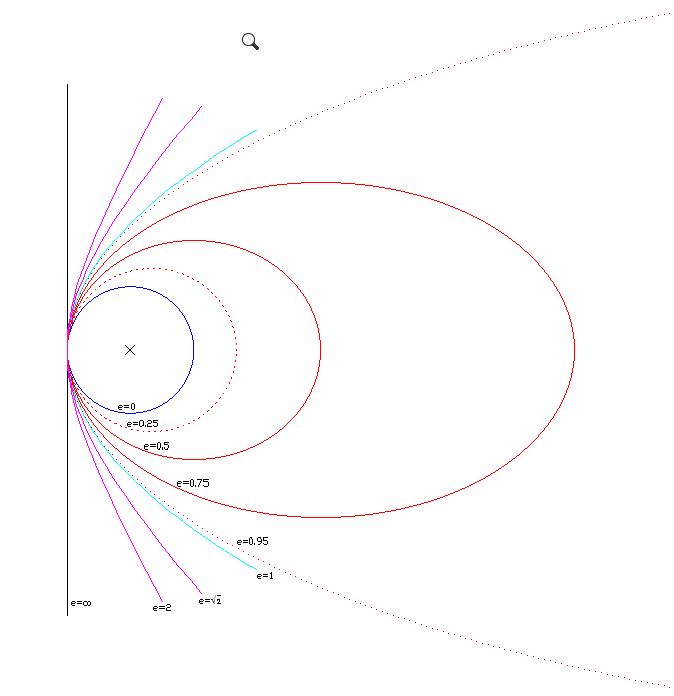
La excentricidad nos indica la forma de la órbita, por ejemplo:
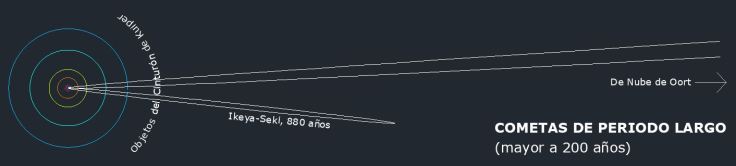
- La mayoría de los planetas del sistema solar tienen una órbita casi circular, los que tienen más excentricidad son Mercurio con 0,2 y Marte con 0,1. Si dibujamos el sistema solar a escala las órbitas nos parecerían circulares.
- Los cometas de periodo corto (< 200 años) tienen órbitas más elípticas, llegando el cometa Halley que nos visita periódicamente a una excentricidad de 0,967.
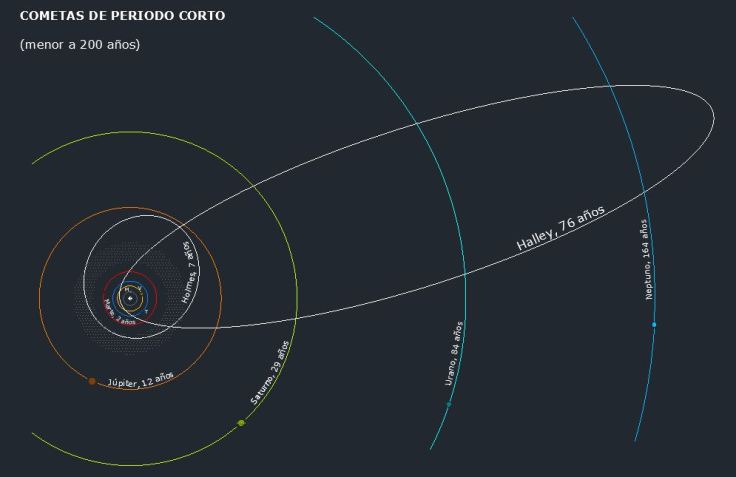
- Los cometas de periodo largo (> 200 años) cuyo origen se sitúa entre el cinturón de Kuiper y la nube de Oort tienen excentricidades próximas a 1 (la parábola) o mayores; por tanto, son órbitas elípticas aplastadísimas o órbitas hiperbólicas de cometas que sólo nos visitan una vez.