
INTRODUCCIÓN
Cuando mi compañero Igor comentó en el correo de la asociación astronómica Sirio que había una persona (Fátima) interesada en descifrar un instrumento llamado astronógrafo inmediatamente llamó mi atención y me ofrecí a colaborar en el proyecto. En aquel momento estaba creando esta página web que fue abandonada totalmente para centrarme en este interesante instrumento.
Este proyecto fue iniciado por Fátima Mª García Doval que fue directora del Centro de Educación Especial “Manuel López Navalón” de Santiago de Compostela, después nos sumamos José Ángel Abraldes Rodeyro, director del Centro de Recursos Educativos de la ONCE en Pontevedra y yo. Agradezco a Fátima su intuición y su tesón por llevar a cabo este proyecto para descifrar el astronógrafo de Navalón, de ella y de José Ángel he recibido su total colaboración y apoyo durante todas las fases del proyecto. También agradecemos la colaboración del museo Tiflológico de la ONCE en Madrid que nos proporcionó diferentes fotografías del instrumento y la cesión del astronógrafo de 1884 para la comunicación aceptada para el Congreso Estatal de Astronomía de A Coruña 2020/2021.
Este instrumento fue realizado por Manuel López Navalón, primer director del Colegio Regional de Sordomudos y Ciegos del Distrito Universitario de Santiago de 1864 a 1902 (hoy CEE Manuel López Navalón). En realidad hizo tres astronógrafos de los que se conservan dos, uno de 1882 y otro de 1884, instrumentos de época madura después de veinte años realizando multitud de aparatos para incentivar el aprendizaje de sus alumnos en diversas materias, muchos de ellos presentados y premiados en exposiciones regionales e internacionales de los que desgraciadamente sólo quedan algunas descripciones. Ya en 1867 había empezado a trabajar con modelos con listoncitos y bisagras para sus clases de dibujo para ciegos, primero en 2D y luego realizando figuras en 3D, posteriormente utilizaría alambres que se insertan en agujeros, elementos que también están presentes en el astronógrafo.
El astronógrafo es un instrumento didáctico ideado para que las personas ciegas colocando una serie de alambres pudieran resolver diferentes problemas de geografía astronómica. Escritos de la época ya enumeran sus posibles usos. Hay que tener en cuenta que durante el transcurso del tiempo el astronógrafo se dejó de utilizar perdiéndose el método de manipulación para su uso que inicialmente se había realizado oralmente. Contenía dos tablillas Braille cuya traducción parecía no tener ningún sentido. Además no estaba claro que alambres y elementos auxiliares correspondían a cada uno de los astronógrafos. Hoy se pueden ver y tocar en en el Museo Tiflológico Nacional de la ONCE.
El proyecto de descifrado de este instrumento se ha presentado en el XXIV Congreso Estatal de Astronomía de A Coruña celebrado, después de ser aplazado, del 9 al 12 de octubre 2021. Tenéis unos vídeos cortitos resumen de las distintas jornadas en el canal de la agrupación Ío que organizó el congreso; nosotros salimos en el de la cuarta jornada (martes 12) del minuto 1:15 a 1:32.
A continuación se presenta el proyecto de investigación al completo. En primer lugar la historia de Navalón y sus instrumentos contada por Fátima en la conferencia de la Jornada «STEM a l’Espai» organizada por «el Departament d’Educació i el campus Baix Llobregat de la Universitat Politècnica de Catalunya». En segundo lugar se presenta un artículo de José Ángel titulado «Más allá del Braille». En tercer lugar explicaré todo el proceso de traducción, descifrado y usos de los dos astronógrafos conservados.
MANUEL LÓPEZ NAVALÓN
Por Fátima Mª García Doval, docente en la Xunta de Galicia y experta en educación y accesibilidad. Co-directora del proyecto ACCEGAL.
3.2 ESFERA ARMILAR TERRESTRE Y CELESTE
Los elementos móviles de latón que acabaron mezclados de los dos astronógrafos (al dejar de usarse con el paso del tiempo) son los siguientes:
- Alambres en forma de arcos (la mayoría semicirculares)
- Varillas rectas con escarpias
- Puntos cardinales
- Bolitas y chinchetas

Algunos de los arcos y una varilla recta tenían divisiones en su longitud, estas se realizaron mediante incisiones sobre el latón; de esta manera una persona ciega podía percibirlas y emplearlas para los diferentes problemas de geometría astronómica que veremos posteriormente. Por último:
- Alambres en forma de arcos con escarpias (la mayoría no semicirculares)


Los arcos semicirculares formarían claramente las líneas imaginarias de la esfera terrestre y celeste (semiesfera armilar) nombrada en los escritos de la época. Los arcos y varilla que tienen marcas permitirían hacer subdivisiones angulares de las líneas imaginarias más importantes como comentaré después. Pero los alambres rectos y los curvos con escarpias no se les veía un uso claro, llegando en un primer momento a pensar que formaban parte de otro instrumento perdido de Navalón, el planímetro, en el que también utilizaba alambres para las clases de dibujo con sus alumnos ciegos.
La primera tarea con estos elementos móviles consiste en un análisis sobre las imágenes facilitadas por la ONCE (algunas solicitadas con regla), posteriormente se realizarían comprobaciones directas. Se utilizan programas de CAD para realizar un estudio dimensional de cada elemento y valorar su encaje en el círculo de taladros de ambos astronógrafos.
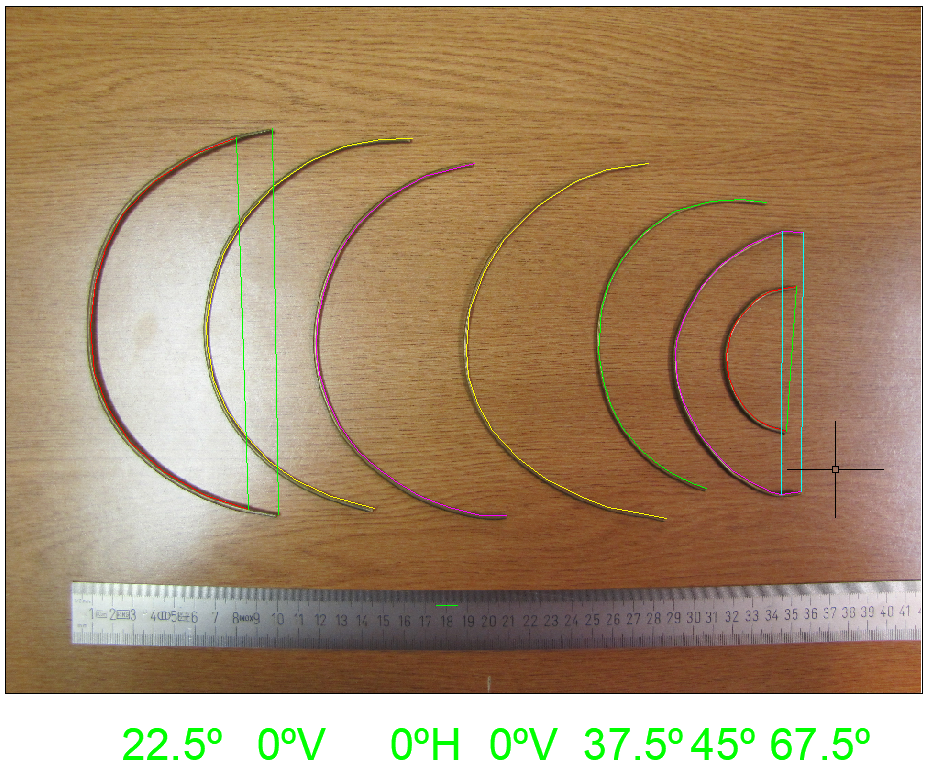
Se establece una relación de los arcos que encajarían en el círculo del astronógrafo mejorado con diferentes paralelos de esfera terrestre o celeste: 0º (ecuador), 22,5º (trópico), 37,5º, 45º y 67,5º (círculo polar). También tendríamos otro arco para simular un meridiano.
El círculo de taladros, un aro de latón en el astronógrafo mejorado, contiene 48 taladros que se corresponden, por tanto, con divisiones de 7,5º (círculo graduado). Esto permitía a Navalón hacer una aproximación bastante aceptable para indicar los trópicos en 22,5º en su modelo armilar de esfera terrestre y celeste (frente a los 23,5º más exactos) y consecuentemente los 67,5º para los círculos polares.
Utilizando los resaltes del reloj que corresponden a 15º los alumnos de Navalón podían contar rápidamente en este círculo graduado y utilizando un taladro intermedio sumar 7,5º más para poder colocar todos esos paralelos en el sitio adecuado, lógicamente esta tarea requeriría algo de práctica.

Al no tener acceso directo a los dos astronógrafos en esta fase de la investigación, se decide realizar modelos virtuales (alambres amarillos en imágenes) para explicar sus posibles usos; posteriormente se comprobaría como estos modelos encajaban casi a la perfección en los instrumentos reales. Esfera terrestre y celeste con sus líneas imaginarias componían las esferas armilares correspondientes, la esfera celeste la veremos posteriormente.
Las medidas tomadas en las imágenes indicaban que el astronógrafo primitivo tenía un diámetro ligeramente inferior, lo cual hacía que los arcos tuvieran dificultad para encajar; en ese momento empiezo a pensar que los alambres rectos podrían encajar en el astronógrafo primitivo creando modelos de la esfera terrestre y celeste en 2D que luego evolucionarían en el mejorado a 3D.

Se comprueba, por tanto, como los alambres rectos definen una proyección ortográfica de la esfera armilar terrestre o celeste, en este caso colocando el alambre recto que simula la eclíptica. Las doce marcas en el ecuador servirían para indicar divisiones de 15º (aunque al proyectarlas no deberían estar equidistantes).
Recordar que estos modelos, tanto el 2D como el 3D, no quedaban montados, los alambres se guardaban en el cajón del instrumento y se sacaban cuando los alumnos de Navalón los utilizaban para «construir» dichos modelos y familiarizarse con todas estas líneas imaginarias de la esfera armilar terrestre y celeste, tanto en las clases como en diferentes demostraciones en diferentes exposiciones regionales e internacionales.
Es probable que con el tiempo alguno de estos alambres haya desaparecido, en el modelo 2D observamos que en el hemisferio norte se han conservado paralelos hasta 75º, en cambio en el modelo 3D aparecen menos paralelos.
Pero había unos alambres que todavía se resistían, los alambres curvos con escarpias, ¿serían de otro instrumento ?; un día en el médico vi una mochila con un logo: ¡ una proyección estereográfica !, sí como la de los mapamundi esos tan chulos y la que también se utilizan en las cartas astronómicas o en la confección de un astrolabio (en la entrada del Astrolabio de estética islámica hay una explicación más técnica sobre esta proyección). Por tanto, comprobé y coincidían bien las medidas, posteriormente enviaría el archivo del modelo virtual a Madrid donde lo replicaron y todo encajaba perfectamente.

Con la esfera armilar terrestre construida podríamos situar un lugar geográfico por sus coordenadas de longitud y latitud e incluso medir distancias de una manera aproximada.
Problema 3: Construir la semiesfera armilar terrestre.
Solución: En primer lugar sacaremos los puntos cardinales de su compartimento y los arcos del compartimento donde hay más (todos lisos salvo dos graduados), los ordenaremos por tamaño y los colocaremos en el astronógrafo en su posición utilizando los resaltes y taladros para medir angularmente: 1º) El más grande y grueso liso que hará de Ecuador (0º) encajado en taladros de izquierda y derecha (6 h en reloj), 2º) Paralelos: 15ºN, trópico de cáncer (22.5ºN), paralelo de 30ºN , paralelo de 37.5ºN (es el arco grueso con 12 subdivisiones) , 45ºN y 45ºS y círculos polares (67.5ºN y 67.5ºS). 3º) Posteriormente cogeremos el arco más grande y grueso graduado que hará de meridiano principal lo pondremos encajado en los taladros superior e inferior, 12 h en reloj (en la foto el meridiano se puso antes en vez de 15ºN).

Problema 4: Situar la ciudad de Constantinopla (hoy Estambul) conocidas su longitud y latitud sobre la esfera armilar terrestre construida en el astronógrafo mejorado. Podemos ver las coordenadas al buscar la ciudad en la wikipedia o en google maps manteniendo pulsado el ratón donde se localiza (estas coordenadas están referidas al meridiano principal de Greenwich que daremos por bueno, aunque la cartografía española de la época de Navalón tome principalmente el meridiano principal por Madrid).
Solución: Las coordenadas de Estambul son 41ºN de latitud y 29ºE de longitud. Si utilizamos el arco graduado (situado en el otro cajón) con 12 divisiones más grande en la posición de meridiano principal y lo abatimos hasta recorrer la coordenada de longitud buscada en el paralelo de 30ºN graduado, dos marcas equivaldrían a 30º de longitud, tan solo tendremos que buscar en este meridiano la latitud deseada para encontrar la posición recordando que cada marca son 15º.
Problema 5: Hallar la distancia entre Constantinopla y otro lugar elegido al azar sobre la esfera armilar terrestre construida en el astronógrafo mejorado.
Solución: Trasladando el arco graduado entre los dos lugares geográficos y sabiendo que la separación entre marcas son 15º (hay 12 subdivisiones en la semicircunferencia) podemos averiguar la separación angular entre los dos lugares. Tan solo nos queda multiplicar por 111 Km que es la distancia que abarca un grado terrestre.
3.3 SOLEAMIENTO: MOVIMIENTOS – CLIMAS ASTRONÓMICOS / LUGARES
Hemos visto como Navalón en sus astronógrafos define una semiesfera armilar primero en proyección (2D) en su astronógrafo primitivo y después en 3D en el astronógrafo mejorado; la diferencia entre la esfera armilar terrestre y la celeste radica en que en esta última podemos colocar la bolita Tierra en el centro e indicamos la eclíptica, por donde «circula el Sol» en su recorrido anual aparente. Por tanto, con la esfera armilar celeste construida podremos hablar de ese movimiento anual aparente que sigue el Sol hacia el este por la eclíptica; colocando el alambre adecuado con sus 12 subdivisiones permite hablar de los doce signos del zodíaco (uno por cada dos marcas en la semieclíptica representada, cada 30º) y, por tanto, de las estaciones, del punto Aries o mejor llamado punto vernal (donde la eclíptica corta al ecuador celeste cuando el Sol sigue un «camino ascendente» respecto al norte astronómico) que dará comienzo a la primavera cuando «lo alcanza el Sol»,…


Pero Navalón no se conforma con que sus alumnos deslicen sus dedos para recorrer esta eclíptica, si no que decide representar el Sol como una bolita de latón para que realice este movimiento aparente guiándolo adecuadamente. Veremos en el siguiente apartado que también realizo otra bolita distinta y más grande para el Sol para utilizarla en modelos en relación con otros astros; pero la más pequeña tiene un saliente de latón para apoyarse en el alambre y seguir su recorrido.
De las bolitas que se conservan solo hay un modelo de cada, lo cual hace pensar que estos «astros» fueron confeccionados para el modelo mejorado, en el que situó dos compartimentos en la parte superior del instrumento para alojarlas junto con los puntos cardinales.

El modelo primitivo tiene también los cuatro taladros centrales que pudieron servir para indicar probablemente los puntos cardinales, aunque de estos también solo se conserva uno de cada. Pero aunque el astronógrafo primitivo no tuviera «astros» le podemos seguir llamando astronógrafo también, dado que al igual que en el mejorado, muestra las horas del soleamiento de lugares de la Tierra en función de su latitud en equinoccios y solsticios (climas astronómicos).

Podemos simular con un alambre el contorno de sombra propia de la Tierra, el terminador (la línea que separa la parte iluminada de la parte que está en sombra propia, el día de la noche). Análisis del soleamiento de la imagen superior:
- A la izquierda: En los equinoccios el Sol está situado coincidente con el ecuador celeste; por tanto, colocamos el terminador perpendicular y vemos como el día y la noche tienen una misma duración de 12 horas (sin contar la refracción atmosférica).
- En el centro: En los solsticios el Sol se «sitúa» formando un ángulo coincidente con la oblicuidad de la eclíptica de la época, 23.5º (22.5º en el astronógrafo ya que contamos subdivisiones de 7.5º por cada taladro); por tanto, si colocamos el terminador perpendicular (los alumnos de Navalón contaban desde el resalte superior al siguiente 15º y colocaban el alambre en el taladro siguiente, 15º+7.5º=22.5º) podemos apreciar como las horas del día en el solsticio de verano (paralelos de color rojo) van creciendo al subir en latitud, empezando con 12 horas en el ecuador y subiendo hasta alcanzar las 24 horas en el círculo polar y hasta los 6 meses en el polo (igualmente sin tener en cuenta la refracción atmosférica). Las horas del día del solsticio de invierno (paralelos de color azul) se puede apreciar como se van reduciendo de un máximo de 12 horas en el ecuador a cero horas a partir del círculo polar (lógicamente equivalen a las horas de la noche del solsticio de verano de la misma latitud y al revés).
Estos modelos 2D o 3D con el terminador colocado en la posición correspondiente al solsticio de verano son los que se utilizaban con la información de las tablillas. Aquí se hablaría de los climas astronómicos, entonces los alumnos de Navalón empezarían con la línea inferior de la tablilla izquierda indicando las horas de soleamiento del solsticio de verano (13 horas), indicarían la latitud correspondiente (16º43’N), buscarían el paralelo correspondiente (en este caso el modelo nos permite buscar el paralelo de 15º correspondiente al resalte superior al del ecuador) e indicarían los lugares geográficos señalados en la tablilla derecha para esa latitud (Cabo Verde, San Luis,…) y repetirían este proceso subiendo cada línea y en el caso del astronógrafo mejorado repitiendo el proceso para el reverso de las tablillas. Este proceso lo podría realizar una persona, o dos si una se dedicara solo a leer los lugares.
En el modelo 3D podemos hasta «contar las horas» de soleamiento que un lugar situado a una latitud de 30º tendría el día del solsticio de verano, su orto y ocaso. Con el terminador colocado perpendicular a la posición del Sol (supuesto a la derecha) en el solsticio de verano podemos contar una hora más para esa latitud al comienzo y al final del día respecto al día de los equinoccios. Si suponemos un lugar moviéndose por ese paralelo (el de 30º que tiene marcas) girado por la Tierra hacia el este, apreciaremos que el Sol saldría a las 5 de la mañana al alcanzar el terminador (hora solar verdadera), culminaría a las doce del mediodía al cruzar el meridiano principal del lugar (aro de taladros, parte derecha) y se pondría a las 7 de la tarde con un total de 14 horas de soleamiento que coincide con el valor dado en la tablilla izquierda para esa latitud.

Pero estos modelos permitían también reflejar el movimiento diario aparente del Sol para una fecha aproximada sobre el modelo celeste (esfera armilar celeste), siguiendo el paralelo correspondiente a la intersección con la posición del Sol en la eclíptica, normalmente en los equinoccios y solsticios.

Si a este modelo le retiramos la bolita central que hacía de Tierra, podemos pasar a un modelo de esfera celeste vista desde el horizonte de un lugar situado en el ecuador (latitud de 0º).

Pero Navalón quiere otra vez ir más allá y realiza un modelo de esfera armilar celeste oblicua para una latitud intermedia de 40ºN. Utiliza un alambre especial a modo de meridiano principal del lugar que está dividido en 8 partes de 20º (en vez de los 15º del resto de alambres), esto facilitaría la disposición táctil del ecuador en 50º (colatitud: 90º-latitud)) y trópicos aproximadamente. Este alambre además tiene los extremos más afilados, lo cual permite reconocerlo de manera táctil más rápidamente.
Con este modelo podemos apreciar el movimiento aparente del Sol en equinoccios y solsticios.

Los alambres oblicuos no se pueden insertan en los taladros debido a su inclinación, simplemente se apoyan sobre tres puntos. En el modelo real podemos observar el ecuador (12 subdivisiones = 12 horas en los equinoccios) y el trópico de Capricornio (9 subdivisiones = 9 horas en el solsticio de invierno). El trópico de Cáncer (15 subdivisiones = 15 horas en el solsticio de verano) falta, es muy probable que se perdiera o fuera substraído. Utilizando las tablillas podemos apreciar una latitud de 41º 21′ a la que corresponden 15 horas de soleamiento máximo, esta latitud es la que está representando de una manera aproximada Navalón; los lugares indicados que corresponderían con este modelo son Barcelona, Roma, Balcanes, Constantinopla, Pekín y Nueva York.
En la imagen siguiente podemos apreciar como el Sol y el resto de astros siguen una trayectoria aparente de este a oeste respecto al horizonte de un lugar, aunque lógicamente sabemos que es la Tierra quién se mueve en dirección opuesta.

Para un lugar situado en una latitud de 0º (ecuador), los astros ascenderán verticalmente por el este y descenderán también verticalmente por el oeste. En una latitud intermedia los astros describirán arcos en la bóveda celeste de este a oeste culminando en el Sur en el hemisferio norte y en el norte en el hemisferio sur.
En estos dos modelos los alumnos de Navalón podían indicar el movimiento aparente del Sol en equinoccios y solsticios respecto al horizonte de un lugar sin más que apoyar la bolita Sol siguiendo el ecuador o trópicos respectivamente. Incluso podrían contar las marcas de cada alambre que corresponderían con las horas diurnas.
Con la esfera armilar terrestre o celeste construida podríamos realizar diferentes problemas para indicar los movimientos aparentes del Sol (tanto anual como diario), signos del zodíaco que atraviesa en su recorrido por la eclíptica, estaciones, climas astronómicos y soleamiento (duración del día, orto, culminación y ocaso).
Problema 6: Con la esfera armilar celeste construida (añadimos Tierra en el centro y el arco graduado lo dispondremos como eclíptica) indica el recorrido anual aparente del Sol con la bolita con saliente apoyándola en el alambre con 12 subdivisiones que hace de eclíptica, indicar los signos del zodiaco que atraviesa e indica en que momento se producen los equinoccios y solsticios.
Solución: Completamos la esfera terrestre para convertirla en celeste, colocaremos la bola Tierra en el centro y el alambre graduado con 12 divisiones que representa a la eclíptica girado 22.5º respecto al ecuador. Apoyaremos la bolita sobre el alambre con incisiones y lo moveremos hacia la derecha (hacia el este), empezando en el ecuador indicaremos el punto aries (punto vernal) donde se produce el equinoccio de primavera y entramos en el signo de Aries, desplazaremos la bolita dos marcas (incisiones) señalando que entra en el signo Tauro, otras dos para entrar en Géminis y otras dos donde se producirá el solsticio de verano con el Sol entrando en el signo de Cáncer. Por detrás tendríamos Cáncer, Leo, Virgo, equinoccio de otoño al entrar en Libra, Scorpio y Sagitario. Delante de nuevo, solsticio de invierno al entrar en Capricornio, Acuario y Piscis.
Problema 7: Con la esfera armilar celeste construida indica el recorrido aparente que el Sol realiza un día determinado como puede ser en los equinoccios y solsticios o en otra fecha.
Solución: Con la bolita con saliente la apoyaremos sobre el alambre que hace de ecuador, la moveremos ahora hacia la izquierda (hacia el oeste) para simular el movimiento aparente del Sol el día de los equinoccios, luego la apoyaremos en el trópico de Cáncer (el superior) para simular el movimiento aparente el día del solsticio de verano, lo mismo para el trópico de Capricornio (el inferior) para el solsticio de invierno, aunque este último alambre pudo perderse. Para buscar la posición de los trópicos sabemos que tenemos que buscar los paralelos de 22.5º.
Problema 8: Con la esfera armilar terrestre construida y la tabla de descifrado de lugares geográficos del anverso o reverso del astronógrafo mejorado, sitúa primero el terminador en equinoccios y luego en solsticios valorando el soleamiento recibido en función de la latitud, posteriormente establece la relación entre los datos de una línea (clima astronómico) de la tabla y el modelo.
Solución: Colocar el terminador coincidente con el meridiano principal para los equinoccios, al deslizar el dedo como si un lugar de la Tierra estuviera rotando en ella, apreciamos la misma duración del día y la noche. En la posición correspondiente al solsticio de verano (22.5º de desvío respecto al meridiano principal, por ejemplo en sentido antihorario) se aprecia como crecen las horas del día respecto al equinoccio y más según ascendemos en latitud. Elegir línea (clima astronómico), con el dato de la latitud buscamos el paralelo correspondiente en el modelo, podemos leer los lugares geográficos y posteriormente las horas de soleamiento correspondientes a esos lugares el día del solsticio de verano simulando con el dedo un lugar geográfico que pasa de la noche al día con el movimiento real de la Tierra hacia el este, podríamos incluso hacer un sencillo cálculo para dar su orto y ocaso al igual que en el problema siguiente).
Problema 9: Construir la esfera armilar celeste oblicua en relación al horizonte de un lugar de latitud 40ºN y simular el movimiento aparente del Sol en equinoccios y solsticios indicando además las hora de orto y ocaso del Sol en hora solar verdadera. Indicar también la altura del Sol en su culminación para estas fechas.
Solución: Colocamos puntos cardinales y posteriormente el meridiano principal del lugar y los arcos de 9 y 12 marcas dispuestos en una posición oblicua ajustando el ecuador a los 50º del meridiano o 40º respecto al cenit (punto más alto del meridiano) hacia el Sur; hemos construido la esfera armilar celeste respecto al horizonte de ese lugar (de 40ºN), ahora podemos deslizar la bolita del Sol por cada uno de estos arcos (el ecuador y trópicos), y tendremos el movimiento aparente del Sol en ese lugar para esas fechas, incluso podemos contar las marcas y saber sus horas de soleamiento o también leerlas en las tablillas. En equinoccios el Sol saldría (orto) a las 6h de la mañana, culminaría a las 12 h al pasar por el meridiano principal del lugar y se pondría (ocaso) a las 6h de la tarde. En el solsticio de verano descontaríamos las 7h30min (la mitad de la duración de soleamiento el solsticio de verano según tablilla para la latitud más próxima de 41º21′,15h) dándonos un orto a las 4:30 a.m. (12-7,5) y un ocaso a las 7:30 p.m. (12+7,5) con un total de 15 h de soleamiento. En el solsticio de invierno descontaríamos 4h30min (la mitad de la duración de soleamiento el solsticio de invierno 24-15=9h) dándonos un orto a las 7:30 a.m. (12-4,5)y un ocaso a las 4:30 p.m. (12+4,5) con un total de 9 h de soleamiento. La hora verdadera del orto, culminación y ocaso del Sol se podrían obtener también retirando el modelo oblicuo y utilizando la esfera del reloj táctil y sus agujas. La altura del Sol en la culminación en los equinoccios será la colatitud (90º-latitud=90º-40º), por tanto, 50º, en el solsticio de verano tendremos 90º (50º+22.5º por oblicuidad de la eclíptica en astronógrafo), por tanto en su culminación el Sol estaría en 72.5º y en el solsticio de invierno 27.5º (50º-22.5º). También podríamos hacer los cálculos más precisos para el valor de las tablillas y una oblicuidad de 23.5º.
Problema 10: Con la esfera armilar terrestre construida y las tablas de descifrado de lugares geográficos del anverso y reverso del astronógrafo mejorado, indica la latitud y los lugares geográficos que se corresponden con un orto solar verdadero a las 3:45 el día del solsticio de verano, posteriormente simula el movimiento de estos lugares.
Solución: Calculamos la duración del día (horas de soleamiento) en el solsticio de verano: 2(12h-3,75h)=2×8,25h= 16,5 horas; buscamos en las tablas y obtenemos una latitud de 51º57′ para un paralelo terrestre que «contiene» a Londres, Bruselas, La Haya, Berlín y Varsovia. Buscaremos el paralelo y lo seguiremos con el dedo.
3.4 FASES DE LA LUNA. ECLIPSES. SISTEMAS DEL UNIVERSO
El astronógrafo mejorado permite utilizar 3 bolitas que simulan la Tierra, la Luna y el Sol. La bolita Sol que vamos a utilizar ahora es la que tiene una aguja incorporada, es la bola más grande, las bolitas Tierra y Luna tienen un tamaño igual. Las tres están realizadas en latón, pero la luna tiene un recubrimiento metalizado frente al dorado de Tierra y Sol, de manera táctil podemos distinguir la Luna de la Tierra por tener una espiga un poco más alta. Con estas tres bolitas podemos simular las fases de la Luna y los eclipses.
Desde nuestra perspectiva geocéntrica , podemos colocar la Tierra en el centro del astronógrafo (una vez retiradas las agujas del reloj táctil), el Sol lo dejaremos en un taladro alineado con uno de los cuatro taladros centrales y la Luna la iremos colocando en cada uno de esos cuatro taladros para simular sus fases.

Podemos suponer, en la imagen superior izquierda, que el aro de taladros estaría a mayor distancia, llegando la luz del Sol a la Luna paralela a la alineación Sol-Tierra, por tanto iluminaría la mitad izquierda desde nuestra perspectiva; con forma de C, pero «la Luna miente» y por tanto tendremos Luna en fase decreciente, girando en sentido antihorario situaremos la Luna en el siguiente taladro, Luna nueva (podemos apreciar como el Sol iluminaría la parte de la Luna por detrás de nuestra perspectiva), movemos al siguiente taladro y Luna creciente (desde la Tierra veríamos una D iluminada), por último Luna llena.
Debido a las diferentes inclinaciones respecto al ecuador de la órbita terrestre (plano de la eclíptica) y de la órbita de la Luna sabemos que los eclipses no se producen siempre que hay Luna nueva o Luna llena; por tanto Navalón coloca el Sol sobre una aguja para elevarlo respecto al ecuador celeste (el aro de taladros), esto permite situar las tres bolitas alineadas espacialmente para simular eclipses.

En la imagen inferior podemos apreciar como cambiando la altura (declinación respecto a la esfera celeste) de la Luna podemos tener Luna llena (los rayos del Sol inciden en la Luna pasando por encima de la Tierra) o eclipse de Luna (interponiéndose la Tierra).

El mismo efecto lo podemos obtener cambiando la altura del Sol (declinación).
Se podrían aprovechar la posición de estas tres bolitas para hablar de los sistemas del Universo, obviando lógicamente otros astros (salvo que los fuéramos situando en hipotéticos círculos cada vez más separados):
- El sistema geocéntrico con la Tierra en el centro, la Luna orbitando en sentido antihorario alrededor y el Sol y los planetas girando más lejos en el mismo sentido.
- El sistema heliocéntrico (ya propuesto por Aristarco en el siglo III a.C.) con el Sol en el centro, la Tierra girando en sentido antihorario (podemos situarla en uno de los cuatro taladros utilizado para las fases de la Luna) y los planetas girando más lejos.
Navalón llega a construir unas chinchetas (se conservan dos) que claramente podrían servir para representar la posición de otros astros (Júpiter, Venus o Marte,…); en este caso el aro de taladros no sería el ecuador si no la eclíptica por donde se mueven próximamente los planetas, la Luna y el Sol desde nuestra perspectiva geocéntrica (no confundir con sistema geocéntrico). Por tanto, teniendo los datos de longitud eclíptica en un día determinado para estos astros se podrían colocar en su posición o al revés encontrar dicha longitud.

Podríamos, por tanto, realizar diversos problemas relacionados con las fases de la Luna, eclipses, sistemas del universo y longitudes eclípticas de los astros.
Problema 11: Colocar la bolita Tierra en el centro, la bolita Luna en uno de los cuatro taladros medios y la bolita Sol (con aguja) en un taladro que se corresponda con las 6 o las 12 del reloj táctil. ¿Qué fase de la Luna se está produciendo?, ¿se está produciendo algún eclipse, si es el caso de que tipo?, ¿que sistema del Universo podríamos representar fijándonos únicamente en estas tres bolitas?
Solución: Una vez situadas las bolitas razonar la fase en función de la posición como se comentó un poco más arriba al hablar de las fases, habrá eclipse si las tres bolitas están alineadas, el tipo dependerá si estamos en fase nueva (eclipse de Sol) o en fase llena (eclipse de Luna), el sistema representado será el geocéntrico o también el heliocéntrico desde una perspectiva geocéntrica.
Problema 12: Colocar la bolita Tierra en el centro y el resto de bolitas (Sol, Luna) y chinchetas (planetas) en el aro de taladros. Indicar la longitud eclíptica de cada astro para ese día.
Solución: Una vez situadas las bolitas y chinchetas sobre el aro de taladros de latón, que en este caso simula la eclíptica, indicar los ángulos respecto al punto Aries (punto vernal) que vamos a suponer en las 12 horas de la parte inferior (doble resalte). Por ejemplo, para la imagen superior, si contamos 15º por cada hora (resalte) en sentido antihorario tendríamos: 2×15º=30º de longitud eclíptica para un planeta (por ejemplo Júpiter), 4×15=60º de longitud eclíptica para otro planeta (por ejemplo Venus o Marte), 8.5×15=127.5º de longitud eclíptica para la posición de la Luna en la eclíptica, por último 16.5×15=247.5º de longitud eclíptica para el Sol.
COROLARIO
En los últimos 30 años, el campo de la astronomía ha dado un salto exponencial debido a los conocimientos adquiridos y, sobre todo, a nuevos instrumentos que obtienen información en otras longitudes de onda distintas a la visible; conocemos el Universo sin verlo. Navalón, en su afán de dar a conocer a sus alumnos sordomudos y ciegos la realidad que les rodeaba, les dotó de los conocimientos y los instrumentos adecuados para comprenderla.
MÁS ALLÁ DEL SISTEMA BRAILLE
Por José Ángel Abraldes Rodeyro, director del Centro de Recursos Educativos de la ONCE en Pontevedra.
El sentido de la vista sin duda es el que proporciona más información e interacción con el mundo que nos rodea, incluso logra anular la capacidad operativa de otros sentidos que se pueden permitir existir en reposo gracias a que la información percibida por los ojos llega a ensombrecer muchas de las sensaciones propias al olfato, el oído y el tacto especialmente. Sólo cuando se está privado de la vista se puede disfrutar de sabores, olores, sonidos o formas que en condiciones normales no se percibirían, dado que es en este momento cuando los restantes cuatro sentidos diligentemente aplican toda su eficiencia.
Las personas ciegas sin duda conocemos bien esta realidad y debemos, mediante la utilización especialmente del tacto y del oído, reemplazar la captación de muchos de los estímulos que las demás personas perciben mediante la vista, todo ello claro está, con el condicionante de que su gran mayoría resultarán inaccesibles para nosotros.
Por ello estos dos sentidos para las personas ciegas son los fundamentales para canalizar la movilidad en espacios interiores como exteriores, la relación social y el contacto con los semejantes, el aprendizaje, el cuidado de la propia persona, …, siendo especialmente el oído el guardián de lo más lejano, protagonizando en gran parte la comunicación y el desarrollo intelectual, quedando el tacto, eso sí, como preciso centinela extendido por todo el cuerpo y con la principal aportación de las manos, a cargo del reconocimiento de nuestro entorno más próximo.
En este punto debemos distinguir el tacto como simple y pasiva percepción cutánea de estímulos y sensaciones como pueden ser el calor o el frío, el dolor, la suavidad o resistencia gruesas, …, y el tacto activo o también llamado “percepción háptica”, que implica la voluntad e intención de conocer, fundamentalmente mediante el contacto manual directo, sensaciones y condiciones como la temperatura, el peso, el movimiento, la forma, la resistencia, la suavidad, la rugosidad, la elasticidad, …, de los cuerpos apreciados.
Conveniente es indicar que el tacto al contrario de la vista, parte de un análisis parcial de un fragmento para alcanzar posteriormente el todo, dado que la segunda, capta un primer clisé para luego acceder a los detalles.
También es preciso subrayar que la percepción cognitiva de los objetos mediante el tacto tiene una menor referencia previa al parecido o recuerdo de una sensación pretérita, lo que, en oposición, sí ocurre a menudo con la percepción visual, que tiene en su repositorio un mayor número de experiencias de referencia a comparar y relacionar.
La capacidad tacto-manipulativa en una persona ciega es fundamental para su autonomía personal en los diferentes entornos vitales, como también lo es para su relación y plena integración social, por lo que este objetivo formativo es una de las principales habilidades a ser entrenadas con los niños ciegos ya desde su más temprana infancia, tanto en la modalidad directa de tacto físico como en la indirecta de manipulación o detección de objetos o del medio, mediante el uso de instrumentos como puede ser el bastón blanco o el uso de juguetes, recursos didácticos, herramientas o el manejo de cubiertos. Por ejemplo, cuando nos enfrentamos a un plato en la comida.
La actividad manipulativa necesariamente debe pasar por fases como: localización, exploración, manipulación, reconocimiento, comparación y organización. Por ello, una baja actividad manual de la persona ciega limitará sobremanera el conocimiento del medio que le rodea.
Fue en la primera mitad del siglo XIX cuando se inventa el sistema de lecto-escritura por Luis Braille, y este alfabeto que se identificará con el apellido de su autor, se generaliza a partir de la segunda mitad del citado siglo, aplicándose de modo progresivo en todos los centros específicos de enseñanza de personas ciegas del mundo, muchas veces integrados en espacios inspirados por la beneficencia hasta la mitad del pasado siglo XX.
El braille fue, es y será por muchos años el mejor sistema de escritura y lectura para las personas ciegas y, su arquitectura rectangular de presencia o ausencia de los 3 puntos que conforman sus 2 líneas paralelas verticales para crear su signo generador de 6 puntos, que a su vez adopta el espacio adecuado para ser apreciado y abarcado por la yema del dedo índice, será favorecido por la inmediatez y versatilidad que la tecnología presente y futura le proporciona y proporcionará, pero siempre se erigirá como el sistema más eficiente y seguro para el acceso a la educación, a la cultura y a la vida independiente.
A menudo el material didáctico específico para las personas ciegas ha debido ser diseñado y reproducido de manera personal y artesanal, siendo muy poco frecuente poder acceder a recursos estándar adecuados y con bajo coste, que permitan también ser utilizados por los carentes de vista. Así, materiales como mapas, cuentos, representaciones artísticas, …, deben ser producidos de modo específico para las personas ciegas y en muchas ocasiones sin la ayuda de medios mecánicos o tecnológicos.
Por todo ello debemos concluir que, para que una persona ciega conozca o aprenda, debe principalmente tocar, derribando las múltiples barreras sociales que impiden este extremo, por ello será muy conveniente darle la media vuelta al dicho y aplicar de modo decidido:
¡Lo que se mira, se toca!
DESCIFRADO Y USO DE LOS ASTRONÓGRAFOS
Por Juan Carlos Asensi Marzal, autor de esta página web.
INFORMACIÓN PREVIA
La imagen siguiente muestra a la izquierda el astronógrafo datado en 1882, le llamaremos astronógrafo primitivo y a la derecha el datado en 1884, al que llamaremos astronógrafo mejorado, ambos muestran un reloj en el centro, dos tablillas con puntos Braille a los lados y un cajón con alambres. Los alambres y elementos auxiliares como puntos cardinales y bolas ya comentamos que se mezclaron, A lo largo de esta descripción iremos viendo para que sirven y las diferencias entre ambos astronógrafos.

El astronógrafo mejorado tiene las siguientes dimensiones: 35.9 cm de largo, 28.5 cm de ancho y 5.3 cm de alto. Los dos están realizados con madera y latón.
Para realizar el astronógrafo más antiguo Navalón aprovecho una caja de puros, aparece además la fecha en el reverso de una tablilla como se podrá observar en una foto cuando hablemos de las tablillas.
Además de analizar el astronógrafo mejorado directamente disponíamos de diversas fotografías actuales de los dos astronógrafos conservados.
Pero también existen escritos de la época que nos hablan de la figura de Navalón y los diversos aparatos didácticos que inventó dando incluso descripciones que aunque no son completas técnicamente informan claramente sobre su utilización. Estos textos se pueden consultar en la hemeroteca digital de la Biblioteca nacional de España:
• Revista pedagógica “La escuela moderna”, 1903 páginas 25 a 34
• Periódico “El Mortero”, 1897 Páginas 3 a 5, 9 y 10
Los usos citados son: construcción de esfera terrestre y celeste con sus diferentes líneas imaginarias, situación de un lugar geográfico, estaciones, climas, horas de soleamiento, horizonte de un lugar,…, sistemas del universo, fases de la luna e incluso eclipses.
En la parte final de esta entrada detallaré y razonaré todos estos usos.
1. TRADUCCIÓN DEL BRAILLE DE LAS TABLILLAS
El sistema Braille fue estandarizado en el Congreso Internacional de París en 1878, pero la disposición manual de los clavos de las celdas Braille en el astronógrafo da como resultado que en ocasiones las celdas estén muy juntas, esto unido al uso de abreviaturas que después se averiguaría hizo que los intentos de traducción táctil se volvieran un galimatías sin reconocer palabras entendibles.
En la imagen siguiente se muestran las tablillas de los dos astronógrafos, las del más antiguo coloca puntos Braille por delante (en el anverso) y en el mejorado también por detrás (anverso y reverso).

Por tanto, lo primero que acometí fue una traducción visual del Braille de las tablillas.
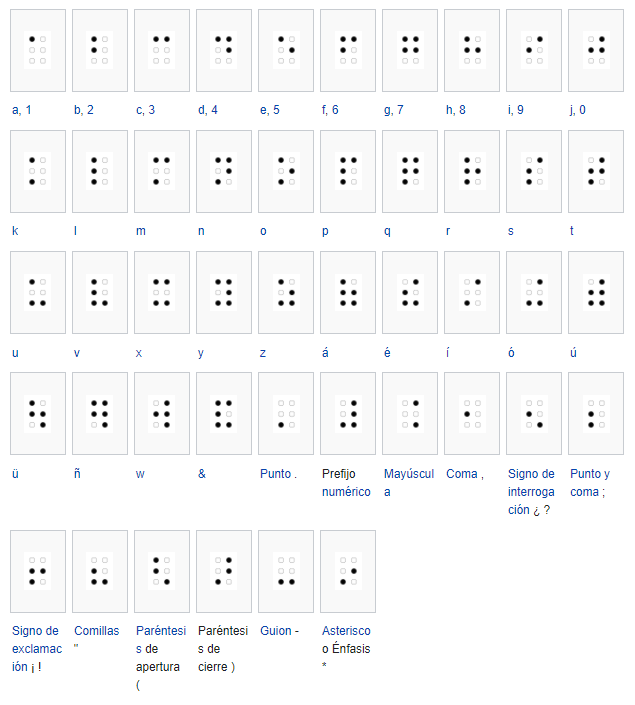
Los escritos citados nos dan pistas mencionando que la tablilla izquierda contiene latitud y horas y la derecha lugares geográficos; por tanto, la tablilla izquierda será la que solo contiene números y la derecha la que solo contiene letras.
Si observamos con detenimiento las tablillas podemos observas los resaltes conseguidos con las cabezas de clavos dorados para formar letras o números en el sistema Braille, veremos también como ya se mencionó que no hay una pauta clara y como esas celdas al estar colocadas manualmente «a ojo» algunas veces están más cerca unas de otras dificultando su traducción. Las tablillas en ocasiones presentan algunas hendiduras para intentar definir los seis puntos de cada celda, dichas hendiduras serían realizadas a posteriori de una manera bastante tosca. También existen algunas incisiones y un agujero más ancho que indica que claramente hubo un clavo. En las tablillas del astronógrafo mejorado al utilizarlas por delante y por detrás añade una chincheta para agarrar con las uñas y darle la vuelta. También en este astronógrafo añade una línea de puntos inferior que junto con la chincheta sirven para clarificar la disposición de la tablilla (arriba-abajo) dado que esta se tiene que andar quitando y volviendo a colocar para utilizar por cada cara.

Por tanto, se ha intentado registrar con rigor también las posibles alternativas para las letras en los casos confusos debido principalmente a la proximidad de las celdas. En la tabla siguiente se indicarán entre paréntesis esas posibles alternativas, en este caso sustituirán a la letra o letras subrayadas. También se indica con doble paréntesis la letra que corresponde a puntos dibujados o muy marcados que parecen ser hechos a posteriori para completar información. Cuando las celdas están claramente separadas se ha indicado con tres espacios o dos, cuando están pegadas cero y casos dudosos un espacio (la letra podrá ir sola, asociarse con las letras de la izda. o las de la dcha).

La traducción visual conseguida en los dos astronógrafos es la siguiente (el anverso de las tablillas se identifica con un 1 y el reverso con un 2):
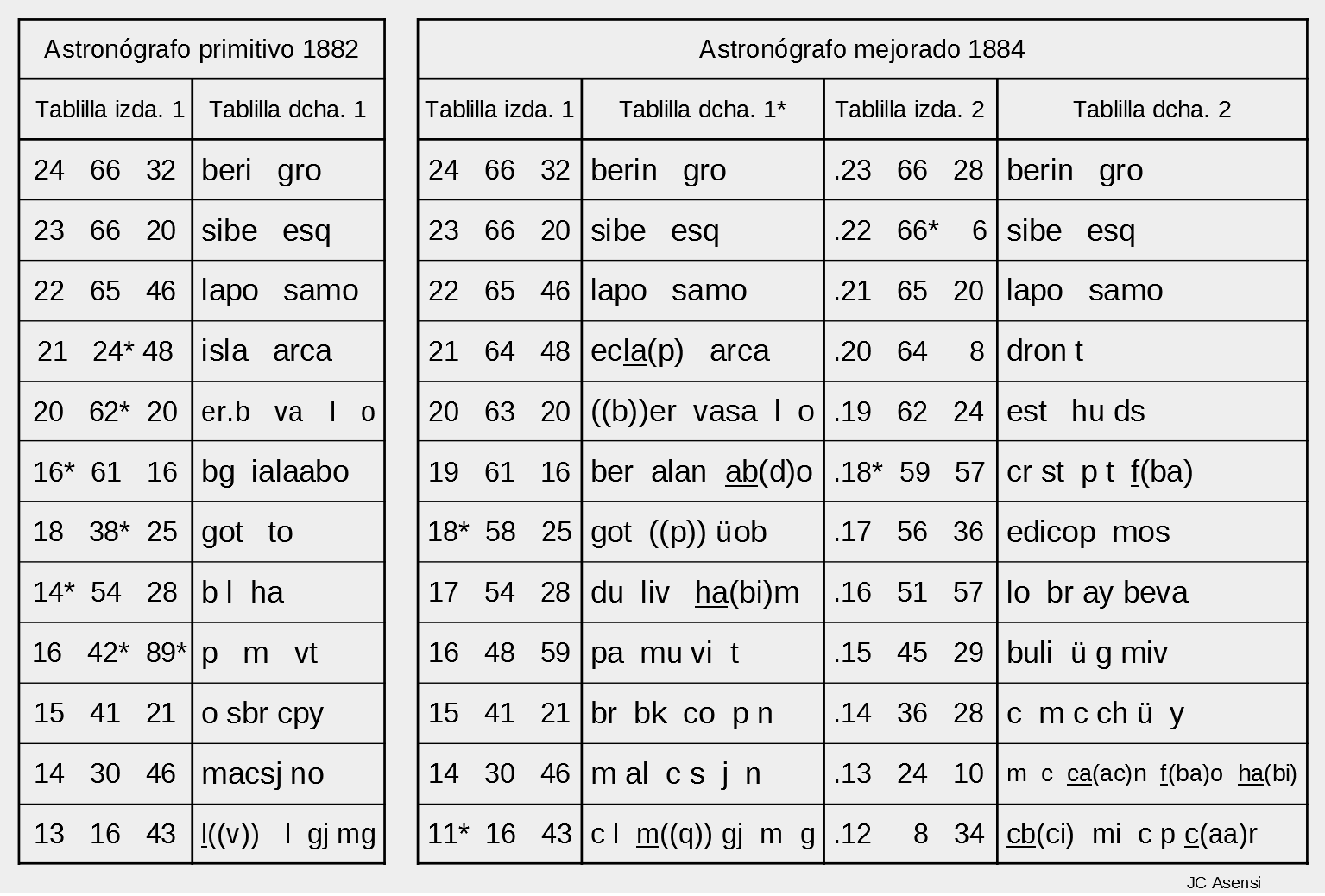
Un análisis inicial de las tablillas traducidas nos indica:

- La tablilla izquierda, como sólo contiene números, ya no lleva la celda estandarizada que se antepone a estos para diferenciarlos de las primeras letras del alfabeto. Esta tablilla consta de 12 líneas (por las dos caras en el astronógrafo de 1884), dando las horas y la latitud en grados y minutos (son 3 columnas de números con 2 cifras). Podemos observar que todas las latitudes pertenecen al hemisferio norte entre 8º34’ y 66º32’ que corresponde con el círculo polar ártico (90º-66º32’=23º28’ valor de la oblicuidad de la eclíptica o inclinación del eje terrestre utilizado por Navalón, aunque en la segunda mitad del XIX el valor más correcto sería 23º27’).
- La tabilla derecha contiene 12 líneas (por las dos caras en el astronógrafo de 1884) que se reconocen como abreviaturas que se corresponderán con lugares geográficos. Algunas líneas tienen claramente dos “palabras” y otras tienen algunos caracteres sueltos no entendibles.
- Se observa que los números y muchas letras de las tablillas del astronógrafo primitivo coinciden con las de la parte que llamaremos anverso en el astronógrafo mejorado, por tanto, la suerte de disponer de dos astronógrafos permitió emparejar más rápidamente números y letras en el anverso y reverso del astronógrafo mejorado (este emparejamiento ya está reflejado en la confección de la tabla anterior). Fijándose mucho se puede observar que la cabeza de una de las chinchetas en una cara de las tablillas del astronógrafo mejorado tiene una forma semiesférica a diferencia de las otras que tienen una forma más plana (esta cara también tiene la línea inferior de puntos que no llega totalmente a la derecha); esto podría facilitar el emparejamiento táctil (para una persona ciega) de esta cara de letras con la cara de números que tienen un punto antepuesto.
- En la tablilla de números se puede ver por comparación como en el astronógrafo primitivo se cometieron muchos errores, siete errores en total (indicados con un asterisco) , en el mejorado sólo uno (la hora 11). Otros asteriscos son aclaraciones, en la hora 18 se puso un asterisco porque es donde se cayó el clavo indicado por un agujero claramente y otros dos asteriscos en valores ordenados claramente por el contexto. Probablemente Navalón primero dibujaría los puntos Braille en un papel y posteriormente colocaría todos los clavos, lo cual requeriría bastante concentración y la posibilidad de cometer errores, que fueron minimizados en el astronógrafo mejorado.
2. DESCIFRADO DE LAS TABLILLAS
Las abreviaturas de 4 letras que aparecen en las latitudes altas eran bastante reconocibles: estrecho de Bering, Siberia, Laponia, samoyedos, Islandia, correspondiéndose con información de lugares geográficos y pueblos indígenas del ártico. También esquimales y Groenlandia con tres letras eran perfectamente reconocibles, pero el resto de abreviaturas con muy pocas letras era un galimatías.
LA PISTA EQUIVOCADA
Se supuso que las horas servían como coordenadas de longitud que junto a la latitud situaban los diferentes puntos geográficos; cada hora (husos horarios) se corresponde con 15º de longitud geográfica, las 12 horas se corresponden con 0º (meridiano de Greenwich), 11h con -15º, 13h con 15º, 14h con 30º,…, 23h=165º, 24h=180º.
Pero los puntos obtenidos no eran lugares geográficos relevantes y tampoco estaban repartidos por todo el globo terráqueo, estos lugares están en el viejo mundo, en el hemisferio norte, desde África hasta el estrecho de Bering, pasando por muchos puntos en territorio ruso. En Google Maps marque los lugares de las supuestas coordenadas geográficas, tanto para la cara superior de las tablillas (rojo) como la cara inferior del astronógrafo mejorado (violeta).
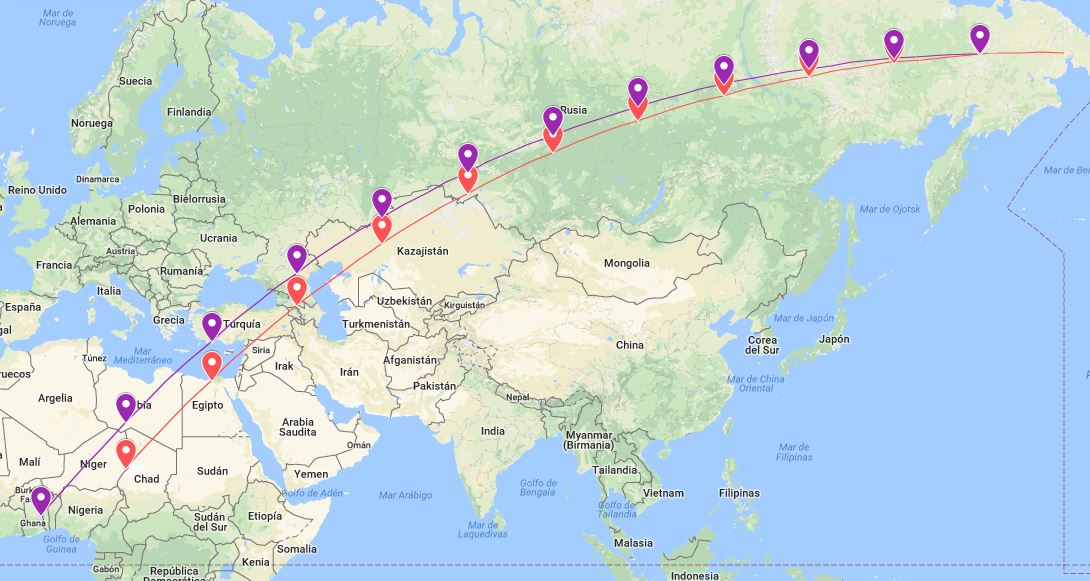
La posición semejaba una trayectoria como si de un eclipse se tratara, llegando incluso a encontrar en la web Nasa Eclipse una trayectoria algo similar en un eclipse ocurrido en 1818.
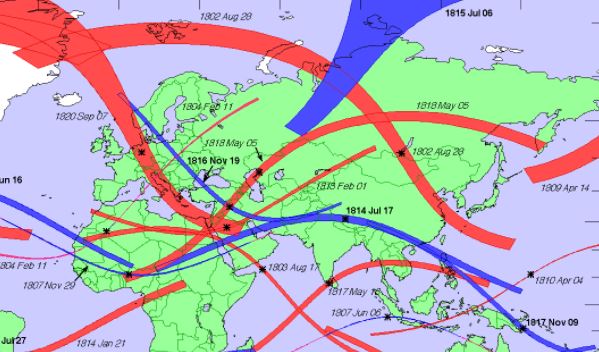
Pronto se vería que este planteamiento estaba totalmente equivocado...
LA ABREVIATURA “GOT”
Un día la abreviatura “got” me empezó a sonar a Göteborg, su longitud no se correspondía con la supuesta longitud de la tablilla, pero al comprobar su latitud esta sí coincidía aproximadamente; entonces, me di cuenta que las abreviaturas podían corresponder con varios lugares de un paralelo terrestre de esa latitud. Al ir comprobando las diferentes latitudes de las tablillas sobre un globo terráqueo (y también en google maps) las abreviaturas se empezaron a materializar en ciudades, una tras otra sobre el mismo paralelo asociado (lugares cercanos admitiendo alguna desviación en latitud, variando como mucho 2º al norte o al sur, 1º equivale a unos 111 Km). Por ejemplo “pa mu vi t” es París, Múnich, Viena y Budapest.
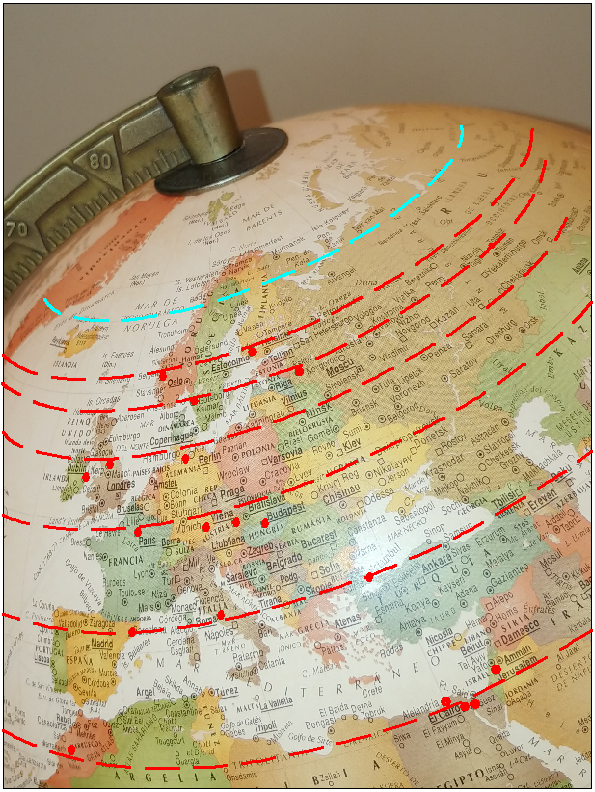
Fue emocionante ir descubriendo decenas de ciudades, y divertido como cuando en la latitud 36º28’ (“c m c ch ü y”) fui “saltando” de isla en isla por el Mediterráneo: Malta… Creta… Chipre… . Las abreviaturas que parecían un galimatías dejaron de serlo y, aunque Navalón para poder indicar abreviadamente más lugares sólo designa cada ciudad por una o dos letras generalmente (y no siempre las dos primeras letras) estas han sido suficientes para localizar los lugares. Estos lugares pertenecen al hemisferio norte y son en su mayoría ciudades, algunas islas, regiones y pueblos indígenas del Ártico y también se indican algunos pasos marítimos naturales.
Muchos lugares salieron muy fácilmente, otros hubo que analizar un poco más. Lógicamente una ciudad que está hoy en un globo terráqueo podría no existir en 1884 o llamarse de otra forma; entonces fuí comprobando en la web, en atlas y mapas históricos. También busqué las ciudades más pobladas , en 1875, Londres era la ciudad más poblada con 4,2 millones de habitantes, París y Nueva York tenían aproximadamente 2 millones, en torno al millón o aproximándose estaban Pekín (Beijing), Berlín, Viena, San Petersburgo y Estambul. Todas estas grandes ciudades aparecen en el astronógrafo de Navalón, también otras capitales y alguna ciudad de menor dimensión. Todos los lugares geográficos discurren a lo largo de diversos paralelos terrestres del hemisferio norte .
En el anverso de los dos astronógrafos, en el que coinciden las horas y latitudes, vemos como en la versión mejorada hace algún pequeño cambio, añadiendo lugares, quitando otros, variando alguna letra. El hecho de disponer de dos versiones del anverso de las tablillas ha ayudado también en la interpretación.
En el astronógrafo mejorado utiliza también el reverso de las tablillas para añadir también latitudes interpoladas de las del astronógrafo anterior para aumentar el número de ciudades y lugares. Se añaden ciudades importantes como Londres, Berlín, San Petersburgo, Cantón o Tokio que no aparecían en el anterior. Un ejemplo de lugares del reverso sería «lo br ay beva», o sea Londres, Bruselas, La Haya, Berlín y Varsovia.
Se ha sustituido la ü que aparecía en tres lugares por una t por considerarlo un error al colocar los puntos Braille en relieve, ya que están situados en ambas letras de manera simétrica respecto al eje vertical de la celdilla Braille, se puede atribuir a un despiste de colocación en la construcción (ya se comento que en las horas y latitudes también hubo algún error).
LA TOPONIMIA EN LA CARTOGRAFÍA DE LA ÉPOCA
En una segunda fase se analizó la cartografía de la época. Se han estudiado mapas de la segunda mitad del siglo XIX atendiendo a su toponimia y también a los exónimos (nombre de un lugar en otras lenguas). En general son mapas que pertenecen a atlas, en esta época muchos eran editados con la nueva técnica de la litografía que conllevaba menos coste económico y de tiempo respecto a las técnicas de grabado tradicionales permitiendo tiradas más grandes, aunque muchos de ellos todavía se coloreaban posteriormente a mano. También las editoriales proporcionaban mapas murales para las instituciones educativas.
No cabe duda que Navalón tuvo que consultar algún atlas y/o mapas murales para indicar los lugares geográficos asociados a los paralelos definidos. Si hacemos una visita virtual al MUPEGA (Museo Pedagógico de Galicia situado en Santiago) o directamente podremos observar que hay mapas murales de finales del XIX y principios del siglo XX que fueron confeccionados por las editoriales siguientes:
- Ed. Justus Perthes
- Ed. Paluzie y Lucena
La editorial Justus Perthes, situada en Gotha (Alemania) desde 1785 hasta hoy, ha realizado los atlas (de gran tamaño y de bolsillo o «de mano») y mapas murales de más calidad desde mediados del XIX y a lo largo de toda la primera mitad del siglo XX. Editores como Stieler, Stüpnagel y Berghaus realizaron diversas ediciones de su atlas, destacado por su rigor científico y la excelente calidad gráfica incluyendo el relieve muy cuidado. En la época analizada todavía no se habían sumado a utilizar la litografía en sus mapas para mantener el nivel de detalle conseguido con el grabado en placas de cobre.
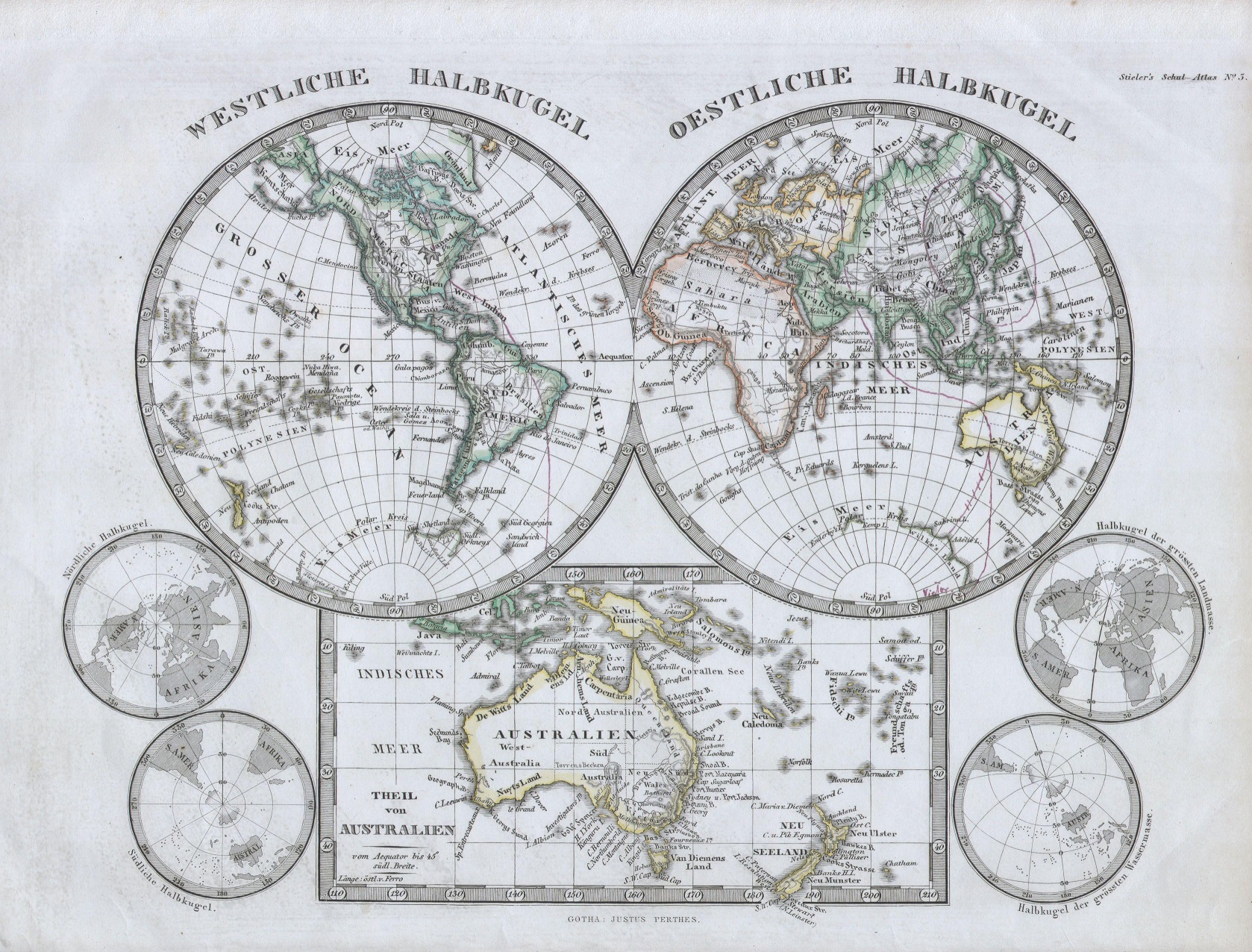
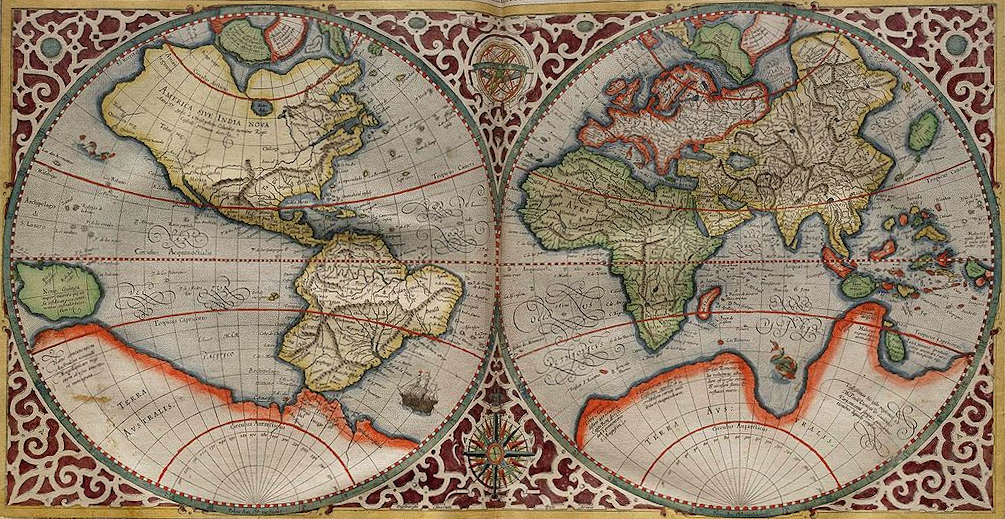
La editorial familiar Esteban Paluzie , situada en Barcelona desde 1840 a 1926, realizó mapas para libros, atlas y murales así como globos terráqueos y celestes «arreglados al meridiano de Madrid». Curiosa es la presentación de sus mapamundis iniciales, la de 1865 de Esteban Paluzie y las de 1879 y 1883 de su hijo Faustino Paluzie, en las que el hemisferio de América se presenta a la derecha del viejo mundo (al este) en vez de a la izquierda (al oeste) que es lo habitual, como lo presentará el nieto José Paluzie (por cierto, un gran agedrecista) como se puede observar en el mapamundi de 1913 situado en el MUPEGA. Esta presentación del mapamundi con el hemisferio de América a la derecha la utilizaron también bastantes cartógrafos franceses en la primera mitad del siglo XIX .
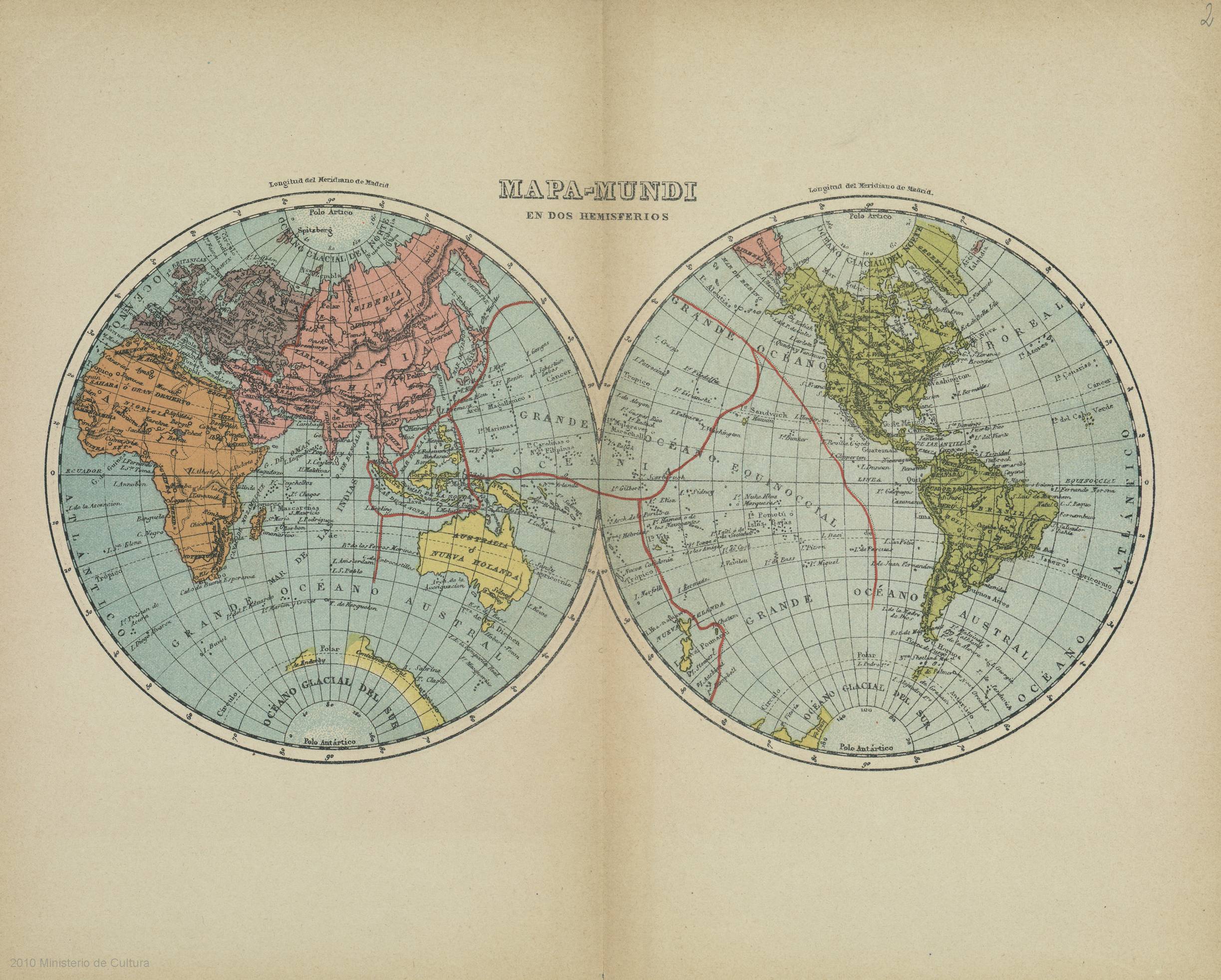
Hay que señalar que Navalón sigue un orden de oeste a este para nombrar los lugares asociados a un paralelo, parte del viejo mundo (incluyendo Islandia) y va añadiendo lugares avanzando hacia el este (rematando en algunos paralelos en Asia, América o Groenlandia).
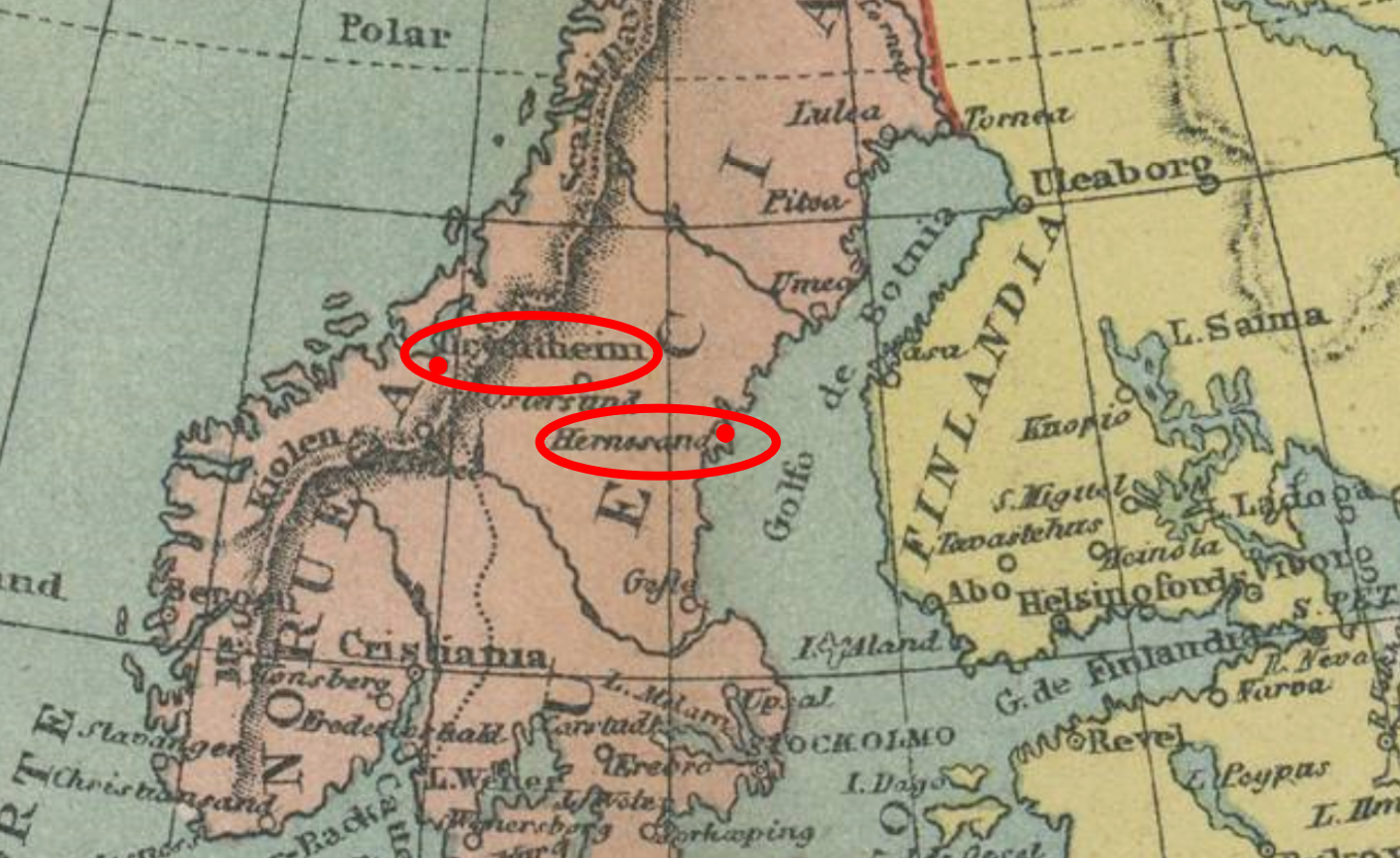
Se ha analizado en concreto cartografía entre 1852 a 1883, mapasmundi y mapas por continentes tanto de estas dos editoriales como también mapas franceses y americanos (Johnson y Mitchel). El análisis de los topónimos y exónimos de dicha cartografía ha sido fundamental para pulir y matizar la primera fase de descifrado con atlas, globos, google maps y atlas históricos actuales, sobre todo para lugares menos conocidos de latitudes más bajas o alguno de latitud alta. Por ejemplo la(s) abreviatura(s) «dron t» se interpreto primero incorrectamente, en atlas actuales e históricos aparecía un lugar Trondheim (la tercera ciudad más poblada de Noruega en 2019) que no se tuvo en cuenta, pero al analizar la cartografía de la época en unos mapas aparecía Trondheim y en otros Drontheim que ahora sí se corresponde totalmente. También Härnösand no se tuvo en cuenta hasta observar en la cartografía de la época Hernosand, Navalón utiliza la abreviatura «er» omitiendo la h para abreviar.
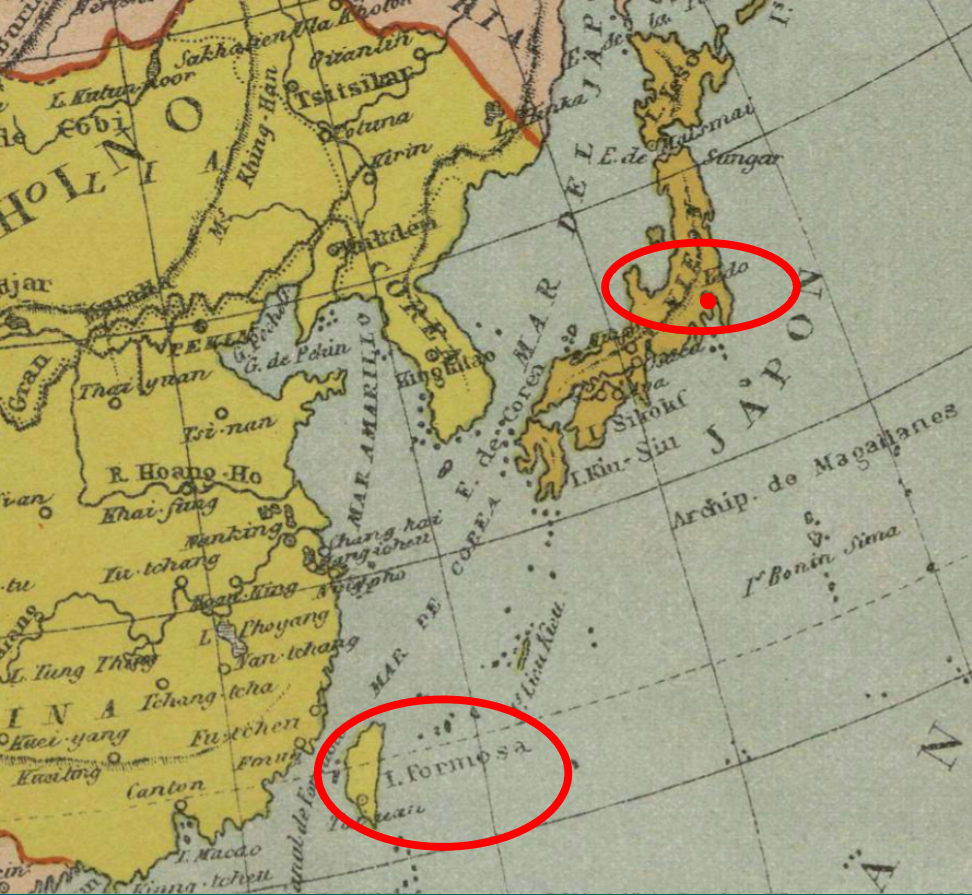
La abreviatura «fo» también se hizo palpable cuando se vio que Taiwan se denominaba Formosa en esa época. Un ejemplo significativo es Tokio, cuyo primer topónimo fue Edo (rebautizada a finales del XIX como Tokyo) , en la cartografía europea y americana aparece con diferentes exónimos, Jedo, Yedo o Yeddo; Navalón utiliza la abreviatura «Y» que podemos ver reflejada en los mapas de Faustino Paluzie y en otros.
En esta segunda fase, por tanto, se consiguieron encontrar o matizar 22 lugares geográficos. En total se han identificado 84 lugares geográficos repartidos por el hemisferio norte, 47 en el anverso de los dos astronógrafos y 43 (6 repetidos) en el reverso del mejorado. Entre estos lugares geográficos hay 63 ciudades, 11 islas , 2 regiones, 2 grupos indígenas del ártico, 2 estrechos geográficos, un monte, un cabo, un volcán y un lago.
A continuación se presenta el descifrado de las abreviaturas obtenido para las tablillas de los dos astronógrafos.
- Descifrado de lugares geográficos del anverso (en la columna de abreviaturas se han indicado para cada latitud en la celda superior las del astronógrafo mejorado y en la inferior las del primitivo):
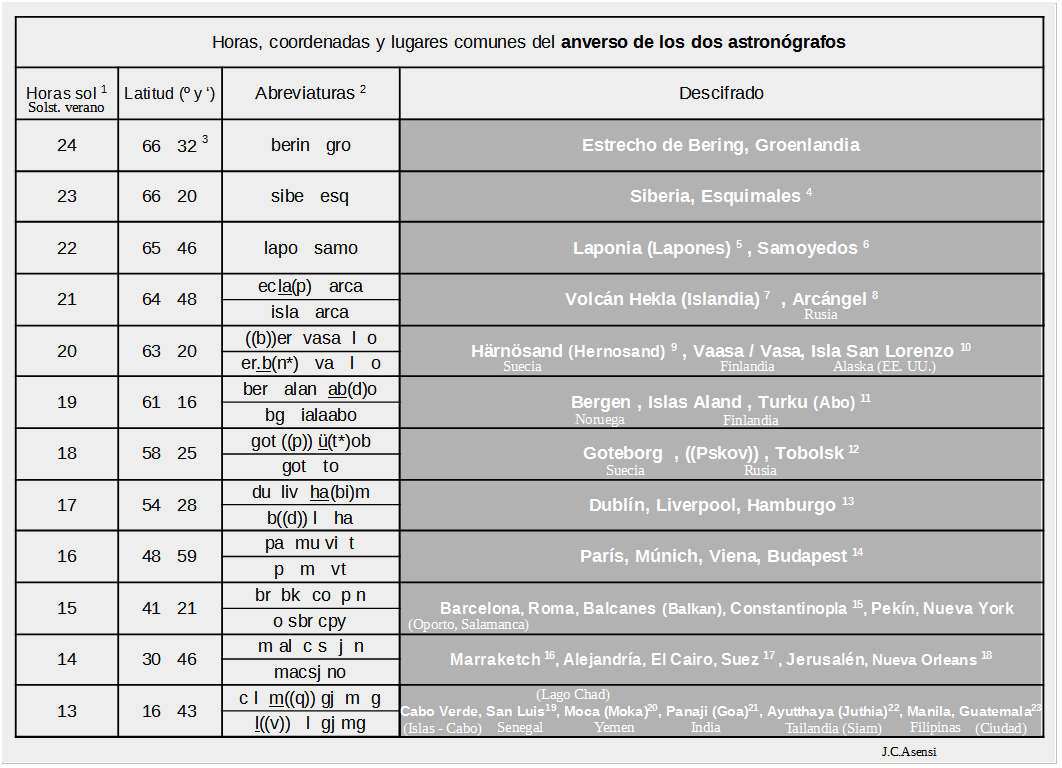
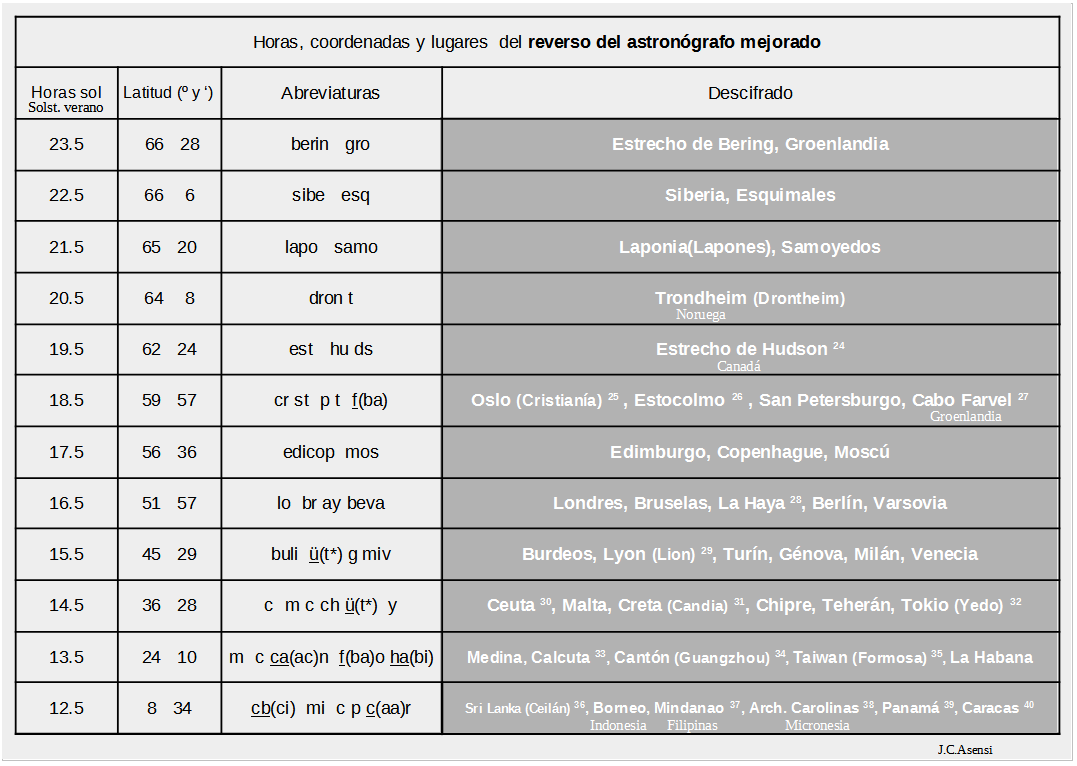
- Descifrado de lugares geográficos del reverso del astronógrafo mejorado:
NOTAS:
- Se indican las horas de sol máximo para esa latitud ( día del solsticio de verano). En los equinoccios de primavera y otoño para cualquier latitud hay 12 horas de sol, el día del solsticio de invierno en cada latitud tendrán las horas que a esta casilla le faltan para llegar a 24 ( Horas S.V. + Horas S.I. = 24 horas).
- Se indican, para cada latitud, en la celda superior las abreviaturas del astronógrafo mejorado y en la inferior las del primitivo (si solo aparece una celda es porque coinciden).
- Latitud del círculo polar ártico (tomado para la época) = 90º – oblicuidad eclíptica (inclinación del eje terrestre respecto a una perpendicular a su plano de traslación en el que órbita alrededor del sol). e = 23º28’ valor de oblicuidad para la segunda mitad del XVIII y primera mitad del XIX; en la época de Navalón (segunda mitad del XIX) el valor correcto sería 23º27’
- Pueblos que habitan las regiones árticas de Norteamérica, Groenlandia y parte de Siberia.
- Región que abarca los territorios del norte de Noruega, Suecia, Finlandia y la península de Kola de Rusia.
- Pueblos nómadas del norte de Rusia.
- En la versión anterior de astronógrafo puso “isla” para referirse a Islandia, pero en el mejorado pone “ecla” para referirse al monte Hekla que contiene un volcán muy activo. En la Edad Media se consideraba una de las puertas al infierno. En la cartografía de la época además de Hekla aparece también como Ekla y otras como Hecla. Navalón no indica Reikiavic, capital de Islandia que estaba en fase de independizarse de Dinamarca; en 1860 contaba con una población de tan solo 1450 habitantes.
- La ciudad de Arcángel tenía el puerto más importante de Rusia hasta la construcción de San Petersburgo en 1703 por Pedro el grande. El nombre fue dado por existir un monasterio ortodoxo ruso “San Miguel Arcángel”. La ciudad se cubre de hielo durante seis meses. Es la ciudad más septentrional que indica Navalón con unas 21 horas de sol en el solsticio de verano y tan solo 3 horas en el solsticio de invierno.
- Fue una ciudad grande con un puerto importante.
- La isla de San Lorenzo fue descubierta por Vitus Bering el día de San Lorenzo de 1728 en una expedición rusa que navegaría también por el estrecho de Bering.
- TurKu (Abo en sueco), ciudad más antigua de Finlandia (antigua capital), perteneció a Suecia y fue anexionada por el Imperio ruso de 1809 a 1917.
- Capital histórica de Siberia.
- Si de “ham” separamos “ha” y “m” tendríamos Hamburgo y Minsk ( hoy capital de Bielorusia) en el mismo paralelo, pero la m esta ligada claramente a las otras dos letras, por lo cual se desecha esta posibilidad.
- Caso especial en que utiliza la última letra, la t; no puso la b para Budapest. Primero pensé que era para diferenciar de Bratislava, pero hasta la primera guerra mundial se llamaba Presburgo; por tanto, esta t la utilizó para remarcar la unión de las ciudades Buda y Pest situadas a cada lado del Danubio, esta unión se produjo en 1873 (en la cartografía de esta época suelen aparecer todavía separadas).
- Estambul, capital del Imperio otomano (también llamado por los occidentales Imperio turco). No fue hasta 1876 que Constantinopla pasó a llamarse Estambul, pero las lenguas occidentales la siguieron llamando Constantinopla hasta 1930.
- Marraketch fue capital histórica de Marruecos. En la cartografía española de la época se le designa Marruecos igual que el país.
- El canal de Suez fue construido de 1859 a 1869 por los franceses. Egipto en 1882 se convertirá en protectorado británico.
- Otras opciones serían Nankín (conocida como la capital del sur de China) y Nueva Delhi que no se contempla porque fue fundada en 1911. Se opta claramente por Nueva Orleans dado que en el astronógrafo primitivo pone la abreviatura no.
- Saint Louis en Senegal, fue la primera ciudad fundada por los Europeos en África occidental, fue capital de la colonia francesa que se empezó a gestar en estos años.
- La ciudad de Moca era famosa por su variedad de café con sabor a chocolate, siendo uno de los puertos más importantes de comercialización de este producto. La entrada al mar rojo era aprovechada por el imperio otomano para establecer aranceles. En el astronógrafo primitivo Navalón puso una “l” en vez de la “m” pudiendo referirse al lago Chad, uno de los mayores del mundo en el siglo XIX.
-
En el siglo XIX Goa se mantuvo como una posesión portuguesa.
-
Juthia fue capital del reino de Siam (Tailandia), también conocida como villa de Siam o simplemente Siam. Otra opción desechada fue Jartum porque implicaba escoger primero Gao en Mali, esta opción se desecha por considerarla de menor entidad.
-
Otra opción sería la isla de Guam (Guaján) que al igual que sus vecinas islas marianas todavía pertenecían a España.
-
Conecta el océano atlántico con la bahía de Hudson y fue navegado por el británico H. Hudson en 1610. Otra opción: est podría referirse a la ciudad sueca Östersund (Oestersund).
-
Oslo era conocido en español como Cristianía hasta 1897, deriva de Christiania (por Christian IV de Dinamarca).
-
Estocolmo aparece en la cartografía española de la época como Stockolmo o Stockholmo.
-
Es el lugar más meridional de Groenlandia.
-
La Haya, sede del gobierno de los Países Bajos, está más próxima al paralelo señalado que Amsterdam que es la capital desde 1830. Navalón nombra La Haya con dos abreviaturas “ay” que prefiere a “ha” para no confundir con Hamburgo.
-
El exónimo Lion aparece en los mapas de la época de la editorial Paluzie.
-
Casablanca no se plantea por la poca entidad que tenía en aquella época. Otra opción es Constantina en Argelia, antes llamada Cirta, fue renovada por el emperador Constantino, pasando posteriormente por manos árabes, otomanas y francesas. Se la conoce también como la ciudad de los puentes. Pero la opción más probable es Ceuta para marcar el límite occidental del Mediterráneo (a partir de aquí Navalón va indicando las islas que rematan en Chipre que marca su límite oriental), en su defecto la segunda opción a considerar sería Cádiz.
-
Creta fue conocida como Candia hasta principios del siglo XX.
-
Edo era la sede del poder desde 1603, en 1868 se traslada el emperador de la antigua capital Kyoto a la nueva y rebautizada Tokyo.
-
Calcuta era la capital de la india británica.
-
Cantón (Guangzhou) era uno de los puertos comerciales más importantes del mundo y contaba ya casi un millón de habitantes en 1825 (momento en que era la tercera ciudad más poblada del mundo). Tuvo el monopolio del comercio con el extranjero que perdió con la apertura de otros puertos como el de Shangai y la cesión de Hong Kong al imperio británico después de las guerras del opio de mediados del XIX.
-
En 1542 los marineros portugueses divisaron una isla a la que llamaron Formosa.
-
Pertenecía en esta época al imperio británico. Otra opción menos probable sería Kumasi (Cumassia) en Ghana, en el golfo de Guinea destacaban por sus riquezas la costa de Marfil francesa y la la costa de Oro (en el actual Ghana) con una colonia inglesa.
-
Borneo y Mindanao aparecen también indicadas como ciudades en cartografía de la época. Mindanao es la segunda isla más grande del archipiélago de las islas Filipinas. Otra opción en vez de Borneo podría ser Benín en Nigeria.
-
En esta época este archipiélago pertenecía a España. Otras opciones descartadas serían la ciudad de Cartago en Costa Rica (tendría más sentido escoger la capital San José) y Colón (población que con Panamá define el ferrocarril transcontinental de 77 km de longitud, de inversión privada americana, operativo desde 1855) por su poca entidad.
-
Fundada en 1519 fue la primera ciudad permanente en costa americana. De 1881 a 1888 se realizó un intento fallido de construcción del canal de Panamá por los franceses, habría que esperar a 1914 en que se inauguró gracias a la inversión de EE. UU.
-
Caracas tenía más entidad que Cartagena de Indias que atravesaba una crisis después de la independencia.
LAS HORAS DE INSOLACIÓN Y LAS LATITUDES
Dado que había varios lugares con diferentes longitudes asociados a un paralelo estaba claro que la columna de las horas no se correspondía con la coordenada de longitud, entonces empecé a pensar que con las horas se refería a las horas de soleamiento máximo ( día del solsticio de verano) correspondientes a la latitud asociada.
Pero quedaban cuestiones más técnicas por resolver, ¿ los valores de latitud a qué se corresponden?, ¿ son las de las ciudades más importantes de cada paralelo indicado o se corresponde con la primera ciudad indicada en cada línea, dando las horas de insolación del S.V. aproximadas y redondeadas a horas?, o ¿las latitudes son las que corresponden a las horas de insolación indicadas?.
Después de analizar las latitudes de todas las ciudades, sólo se encontraron, de las dieciocho líneas que contienen ciudades, dos en las que hay una diferencia igual o menor a un minuto angular en la latitud, sólo coincide San Petersburgo y Milán tienen una diferencia de un minuto. Londres en cambio tiene una diferencia de 27 minutos de arco. Hay que tener en cuenta que a finales del XIX había teodolitos geodésicos y astronómicos que tenían precisiones menores a un segundo angular, por lo que las latitudes ya estaban determinadas en esa época con mucha más precisión.
Se estudia, por tanto, la opción más probable que consiste en que se fijaron primero las horas de insolación y luego se transcribió o calculó la latitud que le corresponde. Lo primero que hice fue mirar en un anuario del observatorio astronómico de Madrid, allí sólo aparecen latitudes exactas cada 10º y sus correspondientes tiempos de insolación, pero hacen referencia a la página web www.roa.es (Real Instituto y Observatorio de la Armada) donde se pueden consultar otras latitudes; en esta página web comprobé que para las latitudes de las tablillas los tiempos de insolación dan mayores a los indicados en los astronógrafos. Hay que considerar que el cálculo del tiempo de insolación tiene en cuenta la refracción atmosférica, por tanto el orto (salida) del Sol se visualiza un poco antes y el ocaso un poco después. Por tanto, comprobé si las horas de insolación indicadas en el astronógrafo estaban calculadas sin tener en cuenta este factor; busqué una libreta de hace 21 años donde me había planteado algunas cuestiones geométricas, ¿a que distancia está la línea del horizonte?, ¿soleamiento en los solsticios y equinoccios?, utilizando geometría descriptiva y trigonometría había sacado una fórmula que me daba las horas de insolación en los solsticios para una latitud determinada o al revés. Comprobé esa fórmula con los valores de Navalón y no me daba, pero repasando el procedimiento vi algún error y rectifiqué la fórmula, entonces empezaron a salir todas las latitudes del astronógrafo de Navalón exactas para una oblicuidad de la eclíptica1 de 23,5º. Por supuesto esta fórmula o alguna similar hace cientos de años que está inventada.
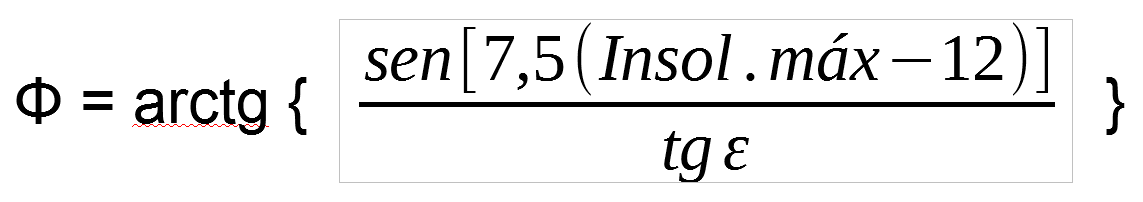
Al aplicar esta fórmula en el astronógrafo mejorado se comprueba que las latitudes corresponden a horas de insolación que van de 12,5 a 23,5 horas. Por tanto, el resalte (clavo) que aparece antes de las horas está indicando media hora adicional, por ejemplo 12h y media consiguiendo ahorrar espacio en la tablilla.

Por tanto, se fijaron primero los valores de la primera columna, las horas de de soleamiento máximo (día del solsticio de verano), sin tener en cuenta la refracción atmosférica.2 Estos valores se indican en el anverso de las tablillas de los dos astronógrafos de 12 h a 24 h, incrementándose cada vez una hora. Las 24h se corresponden con el circulo polar ártico: 66º32’ = 90º – 23º 28’ (oblicuidad de la eclíptica más preciso).3 En el reverso de las tablillas del astronógrafo mejorado van de 12,5 h a 23,5 h. A partir de las horas de insolación máximas, las latitudes fueron transcritas (de algún libro o publicación científica) o calculadas directamente por Navalón. De esta manera quedan fijadas las latitudes (con precisión de grados y minutos) de los paralelos correspondientes a los tiempos de insolación, indicando la mitad de la tablilla en latitudes mayores a 60º, ya que desde 60º hasta la latitud indicada del círculo polar ártico (66º 32’) es cuando la duración del día empieza a aumentar muchísimo más.
NOTAS:
- Ésta tabla refleja un valor para ε ( oblicuidad de la eclíptica, o sea, inclinación del eje terrestre respecto a una línea perpendicular a su plano orbital, o lo que es lo mismo el ángulo que forma el ecuador terrestre respecto a su plano orbital) de 23,5º, salvo para las latitudes de las dos primeras líneas de anverso y reverso que toman 23º29′ salvo la latitud del círculo polar que implica un valor de 23º28′ (valor más preciso correspondiente a la primera mitad del XIX). Posteriormente descubriremos de donde saco Navalón estos valores.
-
Este parámetro depende de la latitud, en latitudes bajas e intermedias la refracción puede suponer que el orto empiece cinco minutos antes y el ocaso cinco minutos después, pero en latitudes mayores a 60º el tiempo de insolación puede incrementarse en más de una hora.
-
El plano orbital de la Tierra varía por perturbaciones orbitales en un ciclo de 41000 años, lo que conlleva que la oblicuidad (media) de la eclíptica varíe entre 22,1º y 24,5º. Actualmente, se encuentra en fase decreciente de su ciclo con un valor de 23º26’ y está reduciéndose 47” por siglo.
LOS CLIMAS ASTRONÓMICOS
Navalón podría haber elegido indicar latitudes en incrementos regulares, cada por ejemplo 5º, y luego calcular las horas de soleamiento máximas asociadas, pero está al revés; esta disposición de horas de soleamiento máximo en incrementos regulares asociándole una latitud es heredera de la división de climas del período grecorromano, fundamentalmente de Ptolomeo.
Clima o klima para los antiguos griegos tenía otra connotación distinta a la actual; el clima se correspondía con zonas, franjas o bandas de la esfera terrestre.
Primero con Parménides (V a. C.) y Aristóteles (IV a. C.) hablaron de 5 climas limitados por los trópicos y por los círculos polares: un clima tórrido (entre trópicos), que pensaban inhabitable debido al calor, al igual que las dos zonas gélidas (entre círculos polares y polos) y por último dos zonas templada habitables, donde se localizaba el ecúmene, la zona habitable y conocida por los griegos.
Posteriormente se empieza a hablar de franjas o bandas relacionadas más con el ecúmene ; asociando climas con la duración del solsticio de verano en incrementos regulares normalmente de media hora. En el renacimiento estas bandas cubrirán también la zona templada del hemisferio sur.

Se fijan paralelos que pasan por ciudades en las que el día más largo tiene esa duración, por ejemplo: 12.5 h (clima 1º), 13 h (clima 2º), 13.5 h (clima 3º), 14 h (clima 4º),… Era una forma de fijar la latitud, posteriormente Hiparco (II a. C.) también trabajará con latitudes geográficas en grados.
En la imagen inferior podemos observar en vez de una tabla un mapa del hemisferio norte que ilustra los climas astronómicos; con paralelos a intervalos de latitud irregulares según los grados, pero regulares en cuanto a indicar incrementos del día más largo (solsticio de verano) de media en media hora como indicó Ptolomeo, aunque se fija algún clima adicional para referirse a localidades más septentrionales no contempladas por Ptolomeo. La duración del solsticio de verano en incrementos regulares se corresponde con el paralelo central de la banda (no se indican los paralelos límite).
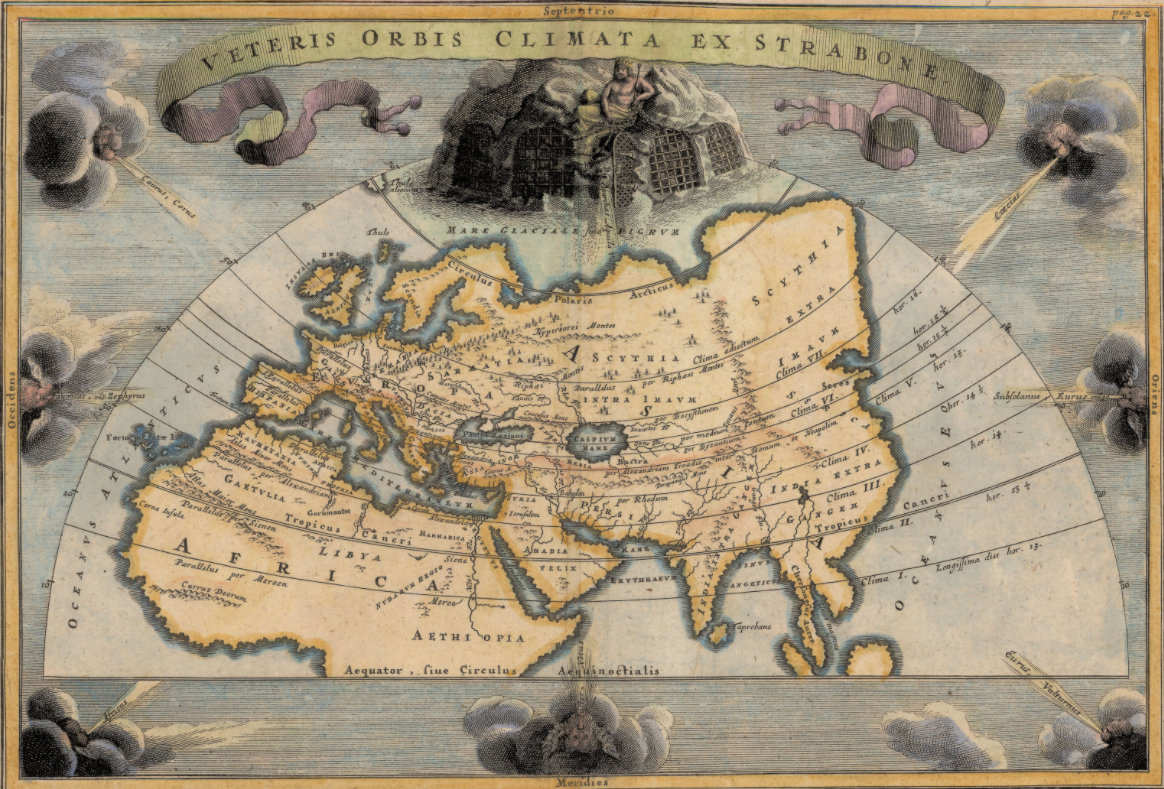
Tanto Hiparco, como Estrabón y Ptolomeo (II d. C.) harán tablas «climata» donde definen ese número variable de climas 11 o 7 en el caso de Ptolomeo, que adopta en el Almagesto un incremento de media hora desde 13 h hasta 16 h (los límites que considera habitables) dando la latitud asociada (en grados y minutos) y una ciudad que define el paralelo y, por tanto, el clima (estas ciudades las fija todas en el meridiano de Alejandría). En las interpretaciones renacentistas de su mapamundi (descrito en su obra Geografía) podemos observar que además de paralelos equidistantes cada 5º aparecen a la izquierda la situación aproximada de los climas, ahora cada quince minutos.

Las tablas «climata» se seguirían haciendo durante mucho tiempo, asociando el clima a la latitud (por horas de soleamiento máximo).
Pero esta visión astronómica del clima ligada exclusivamente a la latitud (zonas latitudinales) sería superada durante el siglo XIX, A. von Humbold introduce zonas térmicas dependientes de latitud y altitud, y van apareciendo otros parámetros entre finales de este siglo y principios del XX, las zonas climáticas se clasificarán dependiendo también de otros parámetros como la precipitación, la cercanía al mar, el viento,…
Cuando Navalón hace sus instrumentos todavía Köppen estaba «cocinando» su clasificación de los climas y algunos libros de Geografía de su época aún presentaban estas tablas «climata» como una información adicional, remarcando que además de los climas astronómicos están los climas físicos.
En concreto, encontré mucho tiempo después de todas las reflexiones anteriores una tabla «climata» con los valores exactos que utilizó Navalón. Aparece en un libro que encontré por internet en la Biblioteca Nacional de España:
«Principios de geografía astronómica, física y política», F. Verdejo Páez. Hay una edición de 1864 y otra de 1871 con la misma tabla.
Ediciones de este libro aparecen también en la biblioteca de la Universidad de Santiago de Compostela, por tanto, como bien apuntó Fátima, también pudo haber consultado el libro allí.
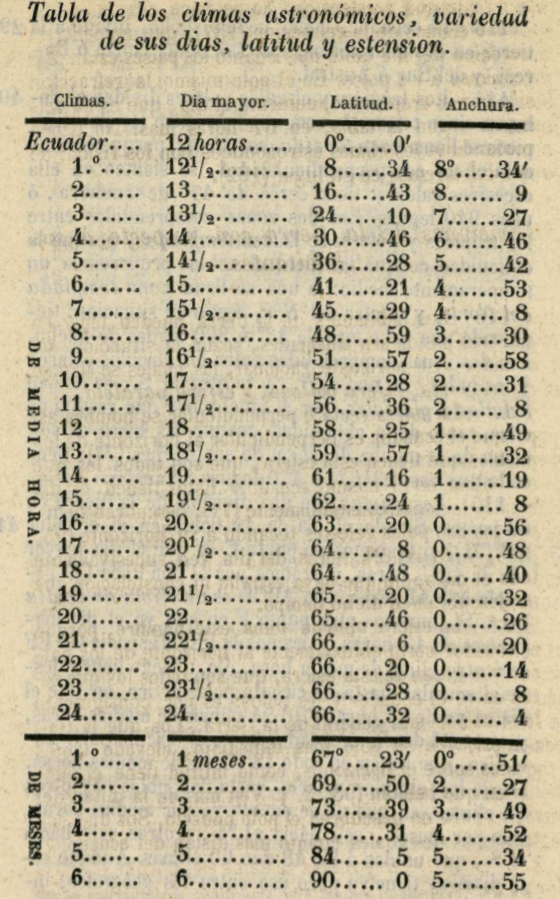
Al lado de esta tabla se remarca que está confeccionada sin tener en cuenta la refracción atmosférica (a mediados del XIX los almanaques nauticos ya incorporan tablas con esta corrección).
Esta tabla también aparece en otro libro similar de 1868, aunque tiene un error en un número. La conclusión es que Navalón utilizó esta tabla de este libro o de otro similar para confeccionar la tablilla izquierda de los dos astronógrafos y posteriormente asigno en esos paralelos (indicados por su latitud) los lugares geográficos escogidos por él para la tablilla derecha (vemos como cambió algunos lugares del astronógrafo primitivo al mejorado). Dado que esos libros de Geografía presenta menos mapas y son más escuetos en cuanto a la toponimia, es lógico pensar que Navalón consulto también algún atlas para seguir la trayectoria de los paralelos y así fijar dichos lugares, las abreviaturas utilizadas apuntan a cartografía española debido a los exónimos empleados, con bastante probabilidad utilizaría un atlas geográfico universal de la editorial Paluzie como ya se comento.
Además Navalón ya utilizó la relación entre la duración del día / noche con la latitud primero en un mapa y luego en un instrumento anterior, el zonógrafo, ambos realizados para alumnos sordos. El zonógrafo, constaba de un rectángulo de cartulina que se movía con una manivela sobre dos círculos, hemisferios y, por tanto, le servía también para explicar los climas astronómicos.
3. USOS DE LOS ASTRONÓGRAFOS
Lo primero que pensé al ver fotos del astronógrafo fue en que los alambres podrían definir una esfera armilar, pero el instrumento es mucho más que eso; dicha esfera armilar permitía que los alumnos ciegos de Navalón pudieran construirla ellos mismos familiarizándose con las líneas imaginarias de la esfera terrestre y celeste, pero además como indican los escritos ya nombrados permitían resolver problemas de geografía astronómica simulando incluso eclipses (algo que parecía exagerado en una primera lectura).
Veremos en los apartados siguientes un desglose de como el astronógrafo es capaz de realizar todo lo indicado en los escritos de la época y como el análisis de su uso ha llevado a diferenciar incluso los alambres que corresponden a cada uno de los astronógrafos.
En el libro comentado de «Principios de geografía astronómica, física y política», F. Verdejo Páez, dentro del apartado de geografía astronómica, aparecen (además de la tabla climata nombrada) toda una serie de problemas de geografía astronómica que el autor resuelve con ayuda de un globo terrestre, aclarando que son soluciones que nos dan de una manera rápida soluciones bastante aproximadas. Navalón resolverá con sus astronógrafos algunos de los problemas citados en dicho libro y mencionados en los escritos de la época de una manera similar. Veremos los diferentes usos desglosados en los apartados siguientes, donde indico diferentes problemas, algunos inspirados en los planteamientos del libro anterior y otros fundamentados en el uso directo de los astronógrafos.
3.1 ESFERA DE RELOJ TÁCTIL
Lo primero que reconocemos en el astronógrafo es una esfera de reloj y sus agujas (una sola en el astronógrafo primitivo). Pero además tenemos los resaltes que permiten identificar las horas (cada 15º). Estas horas están indicadas en números romanos con un ligero resalte en el astronógrafo primitivo y pintadas sin resalte en el astronógrafo mejorado, lo cual indica su carácter complementario frente a los resaltes.
Lógicamente tenemos un instrumento manual cuyo objetivo no es medir el tiempo como un reloj mecánico si no para un uso didáctico. Si colocamos la aguja entre dos resaltes (taladro) tendríamos media hora y entre dos taladros podríamos indicar cuartos de hora. Están
Curiosamente los relojes táctiles no fueron inventados para las personas ciegas; en 1799 Breguet, el famoso relojero, los realizaría para que la alta sociedad pudiera saber la hora ya que en las reuniones sociales estaba mal visto mirar el reloj.


Pero la esfera que utiliza Navalón va en consonancia con el uso del instrumento, por tanto, aparecen 24 horas como en los primeros relojes (astronómicos, de torre,…), antes de que la reducción de sonería forzara un dial de 12 horas. La única aguja nos da la hora con la flecha, simulando la posición aparente del Sol que se desplaza por el ecuador o un paralelo, en su parte opuesta una Luna representa la noche. Suponiendo las 12 de la parte superior como el mediodía, que sería lo más lógico en correlación con el movimiento aparente del Sol en el horizonte de un lugar (como reflejan los astrolabios y los relojes astronómicos que derivan de ellos), tendríamos las 11:45 AM.
El barrido de las agujas de ambos astronógrafos implica un uso independiente de los alambres.


En el astronógrafo mejorado utilizará dos agujas que permiten indicar también minutos, de tal forma que 5 minutos será el avance de dos resaltes (dos horas) al igual que el reloj del observatorio de Greenwich.
Otra posibilidad es utilizar una doble hora para explicar la diferencia de hora en tiempo universal de dos lugares de la Tierra. Recordemos que en el año 1884 se celebra la conferencia del meridiano.
Problema 1: Colocar las agujas del reloj para que marquen las 15:10 en el astronógrafo mejorado.
Solución: Buscaremos de manera táctil el doble resalte superior que nos indica las 12 horas, a partir de aquí buscaremos primero las horas y posteriormente los minutos:
- Desplazaremos el dedo hacia la derecha (sentido horario) contando hasta encontrar el tercer resalte que nos indica las 15 horas y moveremos con la otra mano la aguja pequeña hasta que apunte a este tercer resalte.
- Contaremos hacia el mismo lado cuatro resaltes que equivalen a los 10 minutos buscados y moveremos con la otra mano la aguja grande hasta que apunte a este cuarto resalte.
Problema 2: Dada la hora en un lugar de la Tierra (2:45 PM) hallar la hora en otro lugar situado en un meridiano a 30ºE del primero utilizando el reloj táctil didáctico del astronógrafo mejorado.
Solución: Sabemos que 15º se corresponden con una hora, por tanto 30º con dos que tendremos que sumar para un lugar situado al este, por tanto, 4:45 PM.
3.2 ESFERA ARMILAR TERRESTRE Y CELESTE
Los elementos móviles de latón que acabaron mezclados de los dos astronógrafos (al dejar de usarse con el paso del tiempo) son los siguientes:
- Alambres en forma de arcos (la mayoría semicirculares)
- Varillas rectas con escarpias
- Puntos cardinales
- Bolitas y chinchetas

Algunos de los arcos y una varilla recta tenían divisiones en su longitud, estas se realizaron mediante incisiones sobre el latón; de esta manera una persona ciega podía percibirlas y emplearlas para los diferentes problemas de geometría astronómica que veremos posteriormente. Por último:
- Alambres en forma de arcos con escarpias (la mayoría no semicirculares)


Los arcos semicirculares formarían claramente las líneas imaginarias de la esfera terrestre y celeste (semiesfera armilar) nombrada en los escritos de la época. Los arcos y varilla que tienen marcas permitirían hacer subdivisiones angulares de las líneas imaginarias más importantes como comentaré después. Pero los alambres rectos y los curvos con escarpias no se les veía un uso claro, llegando en un primer momento a pensar que formaban parte de otro instrumento perdido de Navalón, el planímetro, en el que también utilizaba alambres para las clases de dibujo con sus alumnos ciegos.
La primera tarea con estos elementos móviles consiste en un análisis sobre las imágenes facilitadas por la ONCE (algunas solicitadas con regla), posteriormente se realizarían comprobaciones directas. Se utilizan programas de CAD para realizar un estudio dimensional de cada elemento y valorar su encaje en el círculo de taladros de ambos astronógrafos.

Se establece una relación de los arcos que encajarían en el círculo del astronógrafo mejorado con diferentes paralelos de esfera terrestre o celeste: 0º (ecuador), 22,5º (trópico), 37,5º, 45º y 67,5º (círculo polar). También tendríamos otro arco para simular un meridiano.
El círculo de taladros, un aro de latón en el astronógrafo mejorado, contiene 48 taladros que se corresponden, por tanto, con divisiones de 7,5º (círculo graduado). Esto permitía a Navalón hacer una aproximación bastante aceptable para indicar los trópicos en 22,5º en su modelo armilar de esfera terrestre y celeste (frente a los 23,5º más exactos) y consecuentemente los 67,5º para los círculos polares.
Utilizando los resaltes del reloj que corresponden a 15º los alumnos de Navalón podían contar rápidamente en este círculo graduado y utilizando un taladro intermedio sumar 7,5º más para poder colocar todos esos paralelos en el sitio adecuado, lógicamente esta tarea requeriría algo de práctica.

Al no tener acceso directo a los dos astronógrafos en esta fase de la investigación, se decide realizar modelos virtuales (alambres amarillos en imágenes) para explicar sus posibles usos; posteriormente se comprobaría como estos modelos encajaban casi a la perfección en los instrumentos reales. Esfera terrestre y celeste con sus líneas imaginarias componían las esferas armilares correspondientes, la esfera celeste la veremos posteriormente.
Las medidas tomadas en las imágenes indicaban que el astronógrafo primitivo tenía un diámetro ligeramente inferior, lo cual hacía que los arcos tuvieran dificultad para encajar; en ese momento empiezo a pensar que los alambres rectos podrían encajar en el astronógrafo primitivo creando modelos de la esfera terrestre y celeste en 2D que luego evolucionarían en el mejorado a 3D.

Se comprueba, por tanto, como los alambres rectos definen una proyección ortográfica de la esfera armilar terrestre o celeste, en este caso colocando el alambre recto que simula la eclíptica. Las doce marcas en el ecuador servirían para indicar divisiones de 15º (aunque al proyectarlas no deberían estar equidistantes).
Recordar que estos modelos, tanto el 2D como el 3D, no quedaban montados, los alambres se guardaban en el cajón del instrumento y se sacaban cuando los alumnos de Navalón los utilizaban para «construir» dichos modelos y familiarizarse con todas estas líneas imaginarias de la esfera armilar terrestre y celeste, tanto en las clases como en diferentes demostraciones en diferentes exposiciones regionales e internacionales.
Es probable que con el tiempo alguno de estos alambres haya desaparecido, en el modelo 2D observamos que en el hemisferio norte se han conservado paralelos hasta 75º, en cambio en el modelo 3D aparecen menos paralelos.
Pero había unos alambres que todavía se resistían, los alambres curvos con escarpias, ¿serían de otro instrumento ?; un día en el médico vi una mochila con un logo: ¡ una proyección estereográfica !, sí como la de los mapamundi esos tan chulos y la que también se utilizan en las cartas astronómicas o en la confección de un astrolabio (en la entrada del Astrolabio de estética islámica hay una explicación más técnica sobre esta proyección). Por tanto, comprobé y coincidían bien las medidas, posteriormente enviaría el archivo del modelo virtual a Madrid donde lo replicaron y todo encajaba perfectamente.


Con la esfera armilar terrestre construida podríamos situar un lugar geográfico por sus coordenadas de longitud y latitud e incluso medir distancias de una manera aproximada.
Problema 3: Construir la semiesfera armilar terrestre.
Solución: En primer lugar sacaremos los puntos cardinales de su compartimento y los arcos del compartimento donde hay más (todos lisos salvo dos graduados), los ordenaremos por tamaño y los colocaremos en el astronógrafo en su posición utilizando los resaltes y taladros para medir angularmente: 1º) El más grande y grueso liso que hará de Ecuador (0º) encajado en taladros de izquierda y derecha (6 h en reloj), 2º) Paralelos: 15ºN, trópico de cáncer (22.5ºN), paralelo de 30ºN , paralelo de 37.5ºN (es el arco grueso con 12 subdivisiones) , 45ºN y 45ºS y círculos polares (67.5ºN y 67.5ºS). 3º) Posteriormente cogeremos el arco más grande y grueso graduado que hará de meridiano principal lo pondremos encajado en los taladros superior e inferior, 12 h en reloj (en la foto el meridiano se puso antes en vez de 15ºN).

Problema 4: Situar la ciudad de Constantinopla (hoy Estambul) conocidas su longitud y latitud sobre la esfera armilar terrestre construida en el astronógrafo mejorado. Podemos ver las coordenadas al buscar la ciudad en la wikipedia o en google maps manteniendo pulsado el ratón donde se localiza (estas coordenadas están referidas al meridiano principal de Greenwich que daremos por bueno, aunque la cartografía española de la época de Navalón tome principalmente el meridiano principal por Madrid).
Solución: Las coordenadas de Estambul son 41ºN de latitud y 29ºE de longitud. Si utilizamos el arco graduado (situado en el otro cajón) con 12 divisiones más grande en la posición de meridiano principal y lo abatimos hasta recorrer la coordenada de longitud buscada en el paralelo de 30ºN graduado, dos marcas equivaldrían a 30º de longitud, tan solo tendremos que buscar en este meridiano la latitud deseada para encontrar la posición recordando que cada marca son 15º.
Problema 5: Hallar la distancia entre Constantinopla y otro lugar elegido al azar sobre la esfera armilar terrestre construida en el astronógrafo mejorado.
Solución: Trasladando el arco graduado entre los dos lugares geográficos y sabiendo que la separación entre marcas son 15º (hay 12 subdivisiones en la semicircunferencia) podemos averiguar la separación angular entre los dos lugares. Tan solo nos queda multiplicar por 111 Km que es la distancia que abarca un grado terrestre.
3.3 SOLEAMIENTO: MOVIMIENTOS – CLIMAS ASTRONÓMICOS / LUGARES
Hemos visto como Navalón en sus astronógrafos define una semiesfera armilar primero en proyección (2D) en su astronógrafo primitivo y después en 3D en el astronógrafo mejorado; la diferencia entre la esfera armilar terrestre y la celeste radica en que en esta última podemos colocar la bolita Tierra en el centro e indicamos la eclíptica, por donde «circula el Sol» en su recorrido anual aparente. Por tanto, con la esfera armilar celeste construida podremos hablar de ese movimiento anual aparente que sigue el Sol hacia el este por la eclíptica; colocando el alambre adecuado con sus 12 subdivisiones permite hablar de los doce signos del zodíaco (uno por cada dos marcas en la semieclíptica representada, cada 30º) y, por tanto, de las estaciones, del punto Aries o mejor llamado punto vernal (donde la eclíptica corta al ecuador celeste cuando el Sol sigue un «camino ascendente» respecto al norte astronómico) que dará comienzo a la primavera cuando «lo alcanza el Sol»,…


Pero Navalón no se conforma con que sus alumnos deslicen sus dedos para recorrer esta eclíptica, si no que decide representar el Sol como una bolita de latón para que realice este movimiento aparente guiándolo adecuadamente. Veremos en el siguiente apartado que también realizo otra bolita distinta y más grande para el Sol para utilizarla en modelos en relación con otros astros; pero la más pequeña tiene un saliente de latón para apoyarse en el alambre y seguir su recorrido.
De las bolitas que se conservan solo hay un modelo de cada, lo cual hace pensar que estos «astros» fueron confeccionados para el modelo mejorado, en el que situó dos compartimentos en la parte superior del instrumento para alojarlas junto con los puntos cardinales.

El modelo primitivo tiene también los cuatro taladros centrales que pudieron servir para indicar probablemente los puntos cardinales, aunque de estos también solo se conserva uno de cada. Pero aunque el astronógrafo primitivo no tuviera «astros» le podemos seguir llamando astronógrafo también, dado que al igual que en el mejorado, muestra las horas del soleamiento de lugares de la Tierra en función de su latitud en equinoccios y solsticios (climas astronómicos).

Podemos simular con un alambre el contorno de sombra propia de la Tierra, el terminador (la línea que separa la parte iluminada de la parte que está en sombra propia, el día de la noche). Análisis del soleamiento de la imagen superior:
- A la izquierda: En los equinoccios el Sol está situado coincidente con el ecuador celeste; por tanto, colocamos el terminador perpendicular y vemos como el día y la noche tienen una misma duración de 12 horas (sin contar la refracción atmosférica).
- En el centro: En los solsticios el Sol se «sitúa» formando un ángulo coincidente con la oblicuidad de la eclíptica de la época, 23.5º (22.5º en el astronógrafo ya que contamos subdivisiones de 7.5º por cada taladro); por tanto, si colocamos el terminador perpendicular (los alumnos de Navalón contaban desde el resalte superior al siguiente 15º y colocaban el alambre en el taladro siguiente, 15º+7.5º=22.5º) podemos apreciar como las horas del día en el solsticio de verano (paralelos de color rojo) van creciendo al subir en latitud, empezando con 12 horas en el ecuador y subiendo hasta alcanzar las 24 horas en el círculo polar y hasta los 6 meses en el polo (igualmente sin tener en cuenta la refracción atmosférica). Las horas del día del solsticio de invierno (paralelos de color azul) se puede apreciar como se van reduciendo de un máximo de 12 horas en el ecuador a cero horas a partir del círculo polar (lógicamente equivalen a las horas de la noche del solsticio de verano de la misma latitud y al revés).
Estos modelos 2D o 3D con el terminador colocado en la posición correspondiente al solsticio de verano son los que se utilizaban con la información de las tablillas. Aquí se hablaría de los climas astronómicos, entonces los alumnos de Navalón empezarían con la línea inferior de la tablilla izquierda indicando las horas de soleamiento del solsticio de verano (13 horas), indicarían la latitud correspondiente (16º43’N), buscarían el paralelo correspondiente (en este caso el modelo nos permite buscar el paralelo de 15º correspondiente al resalte superior al del ecuador) e indicarían los lugares geográficos señalados en la tablilla derecha para esa latitud (Cabo Verde, San Luis,…) y repetirían este proceso subiendo cada línea y en el caso del astronógrafo mejorado repitiendo el proceso para el reverso de las tablillas. Este proceso lo podría realizar una persona, o dos si una se dedicara solo a leer los lugares.
En el modelo 3D podemos hasta «contar las horas» de soleamiento que un lugar situado a una latitud de 30º tendría el día del solsticio de verano, su orto y ocaso. Con el terminador colocado perpendicular a la posición del Sol (supuesto a la derecha) en el solsticio de verano podemos contar una hora más para esa latitud al comienzo y al final del día respecto al día de los equinoccios. Si suponemos un lugar moviéndose por ese paralelo (el de 30º que tiene marcas) girado por la Tierra hacia el este, apreciaremos que el Sol saldría a las 5 de la mañana al alcanzar el terminador (hora solar verdadera), culminaría a las doce del mediodía al cruzar el meridiano principal del lugar (aro de taladros, parte derecha) y se pondría a las 7 de la tarde con un total de 14 horas de soleamiento que coincide con el valor dado en la tablilla izquierda para esa latitud.

Pero estos modelos permitían también reflejar el movimiento diario aparente del Sol para una fecha aproximada sobre el modelo celeste (esfera armilar celeste), siguiendo el paralelo correspondiente a la intersección con la posición del Sol en la eclíptica, normalmente en los equinoccios y solsticios.

Si a este modelo le retiramos la bolita central que hacía de Tierra, podemos pasar a un modelo de esfera celeste vista desde el horizonte de un lugar situado en el ecuador (latitud de 0º).

Pero Navalón quiere otra vez ir más allá y realiza un modelo de esfera armilar celeste oblicua para una latitud intermedia de 40ºN. Utiliza un alambre especial a modo de meridiano principal del lugar que está dividido en 8 partes de 20º (en vez de los 15º del resto de alambres), esto facilitaría la disposición táctil del ecuador en 50º (colatitud: 90º-latitud)) y trópicos aproximadamente. Este alambre además tiene los extremos más afilados, lo cual permite reconocerlo de manera táctil más rápidamente.
Con este modelo podemos apreciar el movimiento aparente del Sol en equinoccios y solsticios.

Los alambres oblicuos no se pueden insertan en los taladros debido a su inclinación, simplemente se apoyan sobre tres puntos. En el modelo real podemos observar el ecuador (12 subdivisiones = 12 horas en los equinoccios) y el trópico de Capricornio (9 subdivisiones = 9 horas en el solsticio de invierno). El trópico de Cáncer (15 subdivisiones = 15 horas en el solsticio de verano) falta, es muy probable que se perdiera o fuera substraído. Utilizando las tablillas podemos apreciar una latitud de 41º 21′ a la que corresponden 15 horas de soleamiento máximo, esta latitud es la que está representando de una manera aproximada Navalón; los lugares indicados que corresponderían con este modelo son Barcelona, Roma, Balcanes, Constantinopla, Pekín y Nueva York.
En la imagen siguiente podemos apreciar como el Sol y el resto de astros siguen una trayectoria aparente de este a oeste respecto al horizonte de un lugar, aunque lógicamente sabemos que es la Tierra quién se mueve en dirección opuesta.

Para un lugar situado en una latitud de 0º (ecuador), los astros ascenderán verticalmente por el este y descenderán también verticalmente por el oeste. En una latitud intermedia los astros describirán arcos en la bóveda celeste de este a oeste culminando en el Sur en el hemisferio norte y en el norte en el hemisferio sur.
En estos dos modelos los alumnos de Navalón podían indicar el movimiento aparente del Sol en equinoccios y solsticios respecto al horizonte de un lugar sin más que apoyar la bolita Sol siguiendo el ecuador o trópicos respectivamente. Incluso podrían contar las marcas de cada alambre que corresponderían con las horas diurnas.
Con la esfera armilar terrestre o celeste construida podríamos realizar diferentes problemas para indicar los movimientos aparentes del Sol (tanto anual como diario), signos del zodíaco que atraviesa en su recorrido por la eclíptica, estaciones, climas astronómicos y soleamiento (duración del día, orto, culminación y ocaso).
Problema 6: Con la esfera armilar celeste construida (añadimos Tierra en el centro y el arco graduado lo dispondremos como eclíptica) indica el recorrido anual aparente del Sol con la bolita con saliente apoyándola en el alambre con 12 subdivisiones que hace de eclíptica, indicar los signos del zodiaco que atraviesa e indica en que momento se producen los equinoccios y solsticios.
Solución: Completamos la esfera terrestre para convertirla en celeste, colocaremos la bola Tierra en el centro y el alambre graduado con 12 divisiones que representa a la eclíptica girado 22.5º respecto al ecuador. Apoyaremos la bolita sobre el alambre con incisiones y lo moveremos hacia la derecha (hacia el este), empezando en el ecuador indicaremos el punto aries (punto vernal) donde se produce el equinoccio de primavera y entramos en el signo de Aries, desplazaremos la bolita dos marcas (incisiones) señalando que entra en el signo Tauro, otras dos para entrar en Géminis y otras dos donde se producirá el solsticio de verano con el Sol entrando en el signo de Cáncer. Por detrás tendríamos Cáncer, Leo, Virgo, equinoccio de otoño al entrar en Libra, Scorpio y Sagitario. Delante de nuevo, solsticio de invierno al entrar en Capricornio, Acuario y Piscis.
Problema 7: Con la esfera armilar celeste construida indica el recorrido aparente que el Sol realiza un día determinado como puede ser en los equinoccios y solsticios o en otra fecha.
Solución: Con la bolita con saliente la apoyaremos sobre el alambre que hace de ecuador, la moveremos ahora hacia la izquierda (hacia el oeste) para simular el movimiento aparente del Sol el día de los equinoccios, luego la apoyaremos en el trópico de Cáncer (el superior) para simular el movimiento aparente el día del solsticio de verano, lo mismo para el trópico de Capricornio (el inferior) para el solsticio de invierno, aunque este último alambre pudo perderse. Para buscar la posición de los trópicos sabemos que tenemos que buscar los paralelos de 22.5º.
Problema 8: Con la esfera armilar terrestre construida y la tabla de descifrado de lugares geográficos del anverso o reverso del astronógrafo mejorado, sitúa primero el terminador en equinoccios y luego en solsticios valorando el soleamiento recibido en función de la latitud, posteriormente establece la relación entre los datos de una línea (clima astronómico) de la tabla y el modelo.
Solución: Colocar el terminador coincidente con el meridiano principal para los equinoccios, al deslizar el dedo como si un lugar de la Tierra estuviera rotando en ella, apreciamos la misma duración del día y la noche. En la posición correspondiente al solsticio de verano (22.5º de desvío respecto al meridiano principal, por ejemplo en sentido antihorario) se aprecia como crecen las horas del día respecto al equinoccio y más según ascendemos en latitud. Elegir línea (clima astronómico), con el dato de la latitud buscamos el paralelo correspondiente en el modelo, podemos leer los lugares geográficos y posteriormente las horas de soleamiento correspondientes a esos lugares el día del solsticio de verano simulando con el dedo un lugar geográfico que pasa de la noche al día con el movimiento real de la Tierra hacia el este, podríamos incluso hacer un sencillo cálculo para dar su orto y ocaso al igual que en el problema siguiente).
Problema 9: Construir la esfera armilar celeste oblicua en relación al horizonte de un lugar de latitud 40ºN y simular el movimiento aparente del Sol en equinoccios y solsticios indicando además las hora de orto y ocaso del Sol en hora solar verdadera. Indicar también la altura del Sol en su culminación para estas fechas.
Solución: Colocamos puntos cardinales y posteriormente el meridiano principal del lugar y los arcos de 9 y 12 marcas dispuestos en una posición oblicua ajustando el ecuador a los 50º del meridiano o 40º respecto al cenit (punto más alto del meridiano) hacia el Sur; hemos construido la esfera armilar celeste respecto al horizonte de ese lugar (de 40ºN), ahora podemos deslizar la bolita del Sol por cada uno de estos arcos (el ecuador y trópicos), y tendremos el movimiento aparente del Sol en ese lugar para esas fechas, incluso podemos contar las marcas y saber sus horas de soleamiento o también leerlas en las tablillas. En equinoccios el Sol saldría (orto) a las 6h de la mañana, culminaría a las 12 h al pasar por el meridiano principal del lugar y se pondría (ocaso) a las 6h de la tarde. En el solsticio de verano descontaríamos las 7h30min (la mitad de la duración de soleamiento el solsticio de verano según tablilla para la latitud más próxima de 41º21′,15h) dándonos un orto a las 4:30 a.m. (12-7,5) y un ocaso a las 7:30 p.m. (12+7,5) con un total de 15 h de soleamiento. En el solsticio de invierno descontaríamos 4h30min (la mitad de la duración de soleamiento el solsticio de invierno 24-15=9h) dándonos un orto a las 7:30 a.m. (12-4,5)y un ocaso a las 4:30 p.m. (12+4,5) con un total de 9 h de soleamiento. La hora verdadera del orto, culminación y ocaso del Sol se podrían obtener también retirando el modelo oblicuo y utilizando la esfera del reloj táctil y sus agujas. La altura del Sol en la culminación en los equinoccios será la colatitud (90º-latitud=90º-40º), por tanto, 50º, en el solsticio de verano tendremos 90º (50º+22.5º por oblicuidad de la eclíptica en astronógrafo), por tanto en su culminación el Sol estaría en 72.5º y en el solsticio de invierno 27.5º (50º-22.5º). También podríamos hacer los cálculos más precisos para el valor de las tablillas y una oblicuidad de 23.5º.
Problema 10: Con la esfera armilar terrestre construida y las tablas de descifrado de lugares geográficos del anverso y reverso del astronógrafo mejorado, indica la latitud y los lugares geográficos que se corresponden con un orto solar verdadero a las 3:45 el día del solsticio de verano, posteriormente simula el movimiento de estos lugares.
Solución: Calculamos la duración del día (horas de soleamiento) en el solsticio de verano: 2(12h-3,75h)=2×8,25h= 16,5 horas; buscamos en las tablas y obtenemos una latitud de 51º57′ para un paralelo terrestre que «contiene» a Londres, Bruselas, La Haya, Berlín y Varsovia. Buscaremos el paralelo y lo seguiremos con el dedo.
3.4 FASES DE LA LUNA. ECLIPSES. SISTEMAS DEL UNIVERSO
El astronógrafo mejorado permite utilizar 3 bolitas que simulan la Tierra, la Luna y el Sol. La bolita Sol que vamos a utilizar ahora es la que tiene una aguja incorporada, es la bola más grande, las bolitas Tierra y Luna tienen un tamaño igual. Las tres están realizadas en latón, pero la luna tiene un recubrimiento metalizado frente al dorado de Tierra y Sol, de manera táctil podemos distinguir la Luna de la Tierra por tener una espiga un poco más alta. Con estas tres bolitas podemos simular las fases de la Luna y los eclipses.
Desde nuestra perspectiva geocéntrica , podemos colocar la Tierra en el centro del astronógrafo (una vez retiradas las agujas del reloj táctil), el Sol lo dejaremos en un taladro alineado con uno de los cuatro taladros centrales y la Luna la iremos colocando en cada uno de esos cuatro taladros para simular sus fases.

Podemos suponer, en la imagen superior izquierda, que el aro de taladros estaría a mayor distancia, llegando la luz del Sol a la Luna paralela a la alineación Sol-Tierra, por tanto iluminaría la mitad izquierda desde nuestra perspectiva; con forma de C, pero «la Luna miente» y por tanto tendremos Luna en fase decreciente, girando en sentido antihorario situaremos la Luna en el siguiente taladro, Luna nueva (podemos apreciar como el Sol iluminaría la parte de la Luna por detrás de nuestra perspectiva), movemos al siguiente taladro y Luna creciente (desde la Tierra veríamos una D iluminada), por último Luna llena.
Debido a las diferentes inclinaciones respecto al ecuador de la órbita terrestre (plano de la eclíptica) y de la órbita de la Luna sabemos que los eclipses no se producen siempre que hay Luna nueva o Luna llena; por tanto Navalón coloca el Sol sobre una aguja para elevarlo respecto al ecuador celeste (el aro de taladros), esto permite situar las tres bolitas alineadas espacialmente para simular eclipses.

En la imagen inferior podemos apreciar como cambiando la altura (declinación respecto a la esfera celeste) de la Luna podemos tener Luna llena (los rayos del Sol inciden en la Luna pasando por encima de la Tierra) o eclipse de Luna (interponiéndose la Tierra).

El mismo efecto lo podemos obtener cambiando la altura del Sol (declinación).
Se podrían aprovechar la posición de estas tres bolitas para hablar de los sistemas del Universo, obviando lógicamente otros astros (salvo que los fuéramos situando en hipotéticos círculos cada vez más separados):
- El sistema geocéntrico con la Tierra en el centro, la Luna orbitando en sentido antihorario alrededor y el Sol y los planetas girando más lejos en el mismo sentido.
- El sistema heliocéntrico (ya propuesto por Aristarco en el siglo III a.C.) con el Sol en el centro, la Tierra girando en sentido antihorario (podemos situarla en uno de los cuatro taladros utilizado para las fases de la Luna) y los planetas girando más lejos.
Navalón llega a construir unas chinchetas (se conservan dos) que claramente podrían servir para representar la posición de otros astros (Júpiter, Venus o Marte,…); en este caso el aro de taladros no sería el ecuador si no la eclíptica por donde se mueven próximamente los planetas, la Luna y el Sol desde nuestra perspectiva geocéntrica (no confundir con sistema geocéntrico). Por tanto, teniendo los datos de longitud eclíptica en un día determinado para estos astros se podrían colocar en su posición o al revés encontrar dicha longitud.

Podríamos, por tanto, realizar diversos problemas relacionados con las fases de la Luna, eclipses, sistemas del universo y longitudes eclípticas de los astros.
Problema 11: Colocar la bolita Tierra en el centro, la bolita Luna en uno de los cuatro taladros medios y la bolita Sol (con aguja) en un taladro que se corresponda con las 6 o las 12 del reloj táctil. ¿Qué fase de la Luna se está produciendo?, ¿se está produciendo algún eclipse, si es el caso de que tipo?, ¿que sistema del Universo podríamos representar fijándonos únicamente en estas tres bolitas?
Solución: Una vez situadas las bolitas razonar la fase en función de la posición como se comentó un poco más arriba al hablar de las fases, habrá eclipse si las tres bolitas están alineadas, el tipo dependerá si estamos en fase nueva (eclipse de Sol) o en fase llena (eclipse de Luna), el sistema representado será el geocéntrico o también el heliocéntrico desde una perspectiva geocéntrica.
Problema 12: Colocar la bolita Tierra en el centro y el resto de bolitas (Sol, Luna) y chinchetas (planetas) en el aro de taladros. Indicar la longitud eclíptica de cada astro para ese día.
Solución: Una vez situadas las bolitas y chinchetas sobre el aro de taladros de latón, que en este caso simula la eclíptica, indicar los ángulos respecto al punto Aries (punto vernal) que vamos a suponer en las 12 horas de la parte inferior (doble resalte). Por ejemplo, para la imagen superior, si contamos 15º por cada hora (resalte) en sentido antihorario tendríamos: 2×15º=30º de longitud eclíptica para un planeta (por ejemplo Júpiter), 4×15=60º de longitud eclíptica para otro planeta (por ejemplo Venus o Marte), 8.5×15=127.5º de longitud eclíptica para la posición de la Luna en la eclíptica, por último 16.5×15=247.5º de longitud eclíptica para el Sol.
COROLARIO
En los últimos 30 años, el campo de la astronomía ha dado un salto exponencial debido a los conocimientos adquiridos y, sobre todo, a nuevos instrumentos que obtienen información en otras longitudes de onda distintas a la visible; conocemos el Universo sin verlo. Navalón, en su afán de dar a conocer a sus alumnos sordomudos y ciegos la realidad que les rodeaba, les dotó de los conocimientos y los instrumentos adecuados para comprenderla.

Deja un comentario